
الأنماط
احسب الحد النوني للنمط

| الحد | عدد المربعات | الفرق |
| 1 | 5 | 4 |
| 2 | 9 | 4 |
| 3 | 13 | 4 |
| 4 | 17 | 4 |
| 10 | ||
| ن |
هل لاحظت أن الزيادة بين حدين متتالين هي 4 ؟
المتتالية من الدرجة الأولى والصورة العامة لها
an+b
n=1 عندما نعوض
فأن العبارة تصبح
a+b
تساوي الحد الأول في المتتالية
a+b=5
n=2 نعوض عندما
فأن العبارة تصبح
2a+b
تساوي الحد الثاني في المتتالية
2a+b= 9
ثم نقوم بطرح أحدى العبارتين من الأخرى
يكون
a=4
بالتعويض في المعادلة
a+b=5
فان
b= 1
الحد العام
an+b
4n+1
الفكرة أن المتتالية
5 9 13 17 21
الفرق بين حدين متتالين هو 4
ونعلم أن مضاعفات 4 ما يلي
4 8 12 16 20
|
مضاعفات 4 |
|||||
| 4ن | 4 | 8 | 13 | 16 | 20 |
|
حدود المتتالية |
|||||
| ؟ | 5 | 9 | 13 | 17 | 21 |
الحد العام = 4ن + 1
=====================================================
مثال

3 5 7 9 11 13
لاحظ الزيادة بين كل حدين متتالين=2
| الحد | عدد الأشجار | الفرق |
| 1 | 3 | 2 |
| 2 | 5 | 2 |
| 3 | 7 | 2 |
| 4 | 9 | 2 |
| ن |
3 5 7 9 11 13
مضاعفات 2
2 4 6 8 10
|
مضاعفات 4 |
|||||
| 2ن | 2 | 4 | 6 | 8 | 10 |
|
حدود المتتالية |
|||||
| ؟ | 3 | 5 | 7 | 9 | 11 |
الحد العام = 2ن + 1
========================================
أمثلة عندما يكون الفرق بين حدين متتالين غير ثابت

| الحد | عدد المربعات | الفرق1 | الفرق2 |
| 1 | 4 | 5 | 2 |
| 2 | 9 | ||
| 3 | 16 | 7 |
2 |
| 4 | 25 | 9 | 2 |
| العام |
لاحظ أن الفرق الثاني ثابت مما يعني أن المتتالية من الدرجة الثانية في صورة
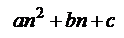
نعوض في الصورة العامة عن n
مرة = 1 ومرة ثانية =2 ومرة ثالثة =3 نحصل على
ونحسب الفرق
الفرق الثابت = 2a
هذا الفرق الثاني في التعويض = الفرق الثاني في الحدود
2 = 2a
ومنها
a=1
نعوض في المقدر
3a+b
الفرق الأول في التعويض= الفرق الأول في حدود المتتالية
3a+b= = 5
حيث ان
a=1
يكون
b=2
a+b+c= الحد الأول = 4
نعوض عن
a ,b
نحصل على
c= 1
الحد العام
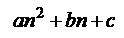
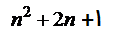
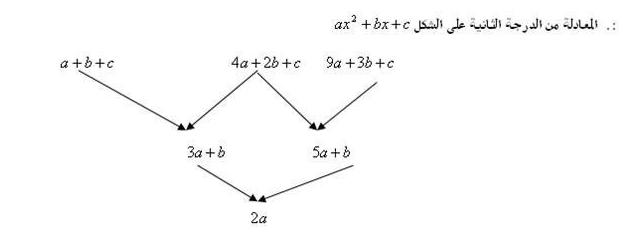
نطبق القاعدة على الحد رقم 3
9+6+1= 16
بالنظر الى النمط يمكن استنتاج القاعدة

الأعداد 1 2 3
النمط 2 3 4
مربعات
(الحدود +1)^2
متطابقة مربع مجموع حدين
(ن+1)^2= ن^2+2ن+1
=============================================================
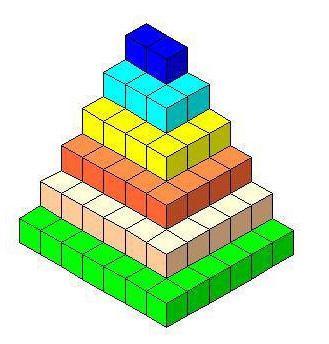
متتاليات من الدرجة الثالثة
| الشكل الرابع | الشكل الثالث | الشكل الثاني | الشكل الأول |
|
73 |
34 |
13 |
4 |
|
|
|
|
|
الرابع بدون تشويش مربعات غير ملونة

الوصف
الحد الرابع: 4 مرات مربع 4 في 4 +مستطيلين 1 في 4 + مربع
الحد الثالث: 3 مرات مربع 3 في 3 +مستطيلين 1 في 3 + مربع
الحد الثاني: 2 مرة مربع 2 في 2 +مستطيلين 1 في 2 +مربع
الحد الأول: مرة واحدة مربع 1 في 1+مستطيلين ( 1في 1) + مربع
| الحد | القيمة |
| 1 | 4 |
| 2 | 13 |
| 3 | 34 |
| 4 | 73 |
| 5 | 136 |
| 6 | 229 |
| الحد | القيمة | فرق1 | ف2 | ف3 |
| 1 | 4
|
9 | 12 | 6 |
| 2 | 13
|
21
|
18 | 6 |
| 3 | 34
|
39 |
24 | 6 |
| 4 | 73 | |||
| 5 | 136 |
63 |
30 |
6 |
| 6 | 229 | 93 |
المتتالية من الدرجة الثالثة
an^3 +bn^2+cn+d
نعوض عن n مرة 1 ومرة 2 ومرة 3 ومرة4 ونحسب الفروق
|
125a+25b+5c+d |
64a+16b+4c+d |
27a+9b+3c +d |
8a+4b+2c+d |
a+b+c+d |
| d1 | 61a+9b+c | 37a+7b+c | 19a+5b+c | 7a+3b+c |
| d2 | 24a+2b | 18a+2b | 12a+2b | |
| d3 | 6a | |||
الفروقات
| فرق1 | ف2 | ف3 |
| 9 | 12 | 6 |
|
21
|
18 | 6 |
|
39 |
24 | 6 |
الفرق الثالث في التعويض= الفرق الثالث في الحدود
6a= 6
a=1
الفرق الثاني في التعويض= الفرق الثاني في الحدود
18a+2b= 12
نعوض عن a=1
b=صفر
الفرق الأول في التعويض= الفرق الأول في الحدود
7a+3b+c=9
نعوض عن a و b ونحسب c
c=2
الحد الأول في التعويض= الحد الأول في الحدود
a+b+c+d
يساوي
4
a+b+c+d= 4
نعوض فنحصل على
d=1
للحصول على القاعدة العامة نعوض في المقدار
an^3 +bn^2+cn+d
عن a , b, c, d
نحصل على
n^3 +2n+1
==============================================================
| الشكل الرابع | الشكل الثالث | الشكل الثاني | الشكل الأول |
|
73 |
34 |
13 |
4 |
|
|
|
الحد الرابع: 4 مرات مربع 4 في 4 +مستطيلين
1 في 4 + مربع
الحد الثالث: 3 مرات مربع 3 في 3 +مستطيلين 1 في 3 + مربع
الحد الثاني: 2 مرة مربع 2 في 2 +مستطيلين 1 في 2 +مربع
الحد الأول: مرة واحدة مربع 1 في 1+مستطيلين ( 1في 1) + مربع
==============================================================
ما قاعدة النمط

بالنظر الى الشكل من الأسفل الى الأعلى وعد المكعبات يجد أن القاعدة
مربع ن في ن
وفوقه
ن(ن-1)
وفوق ذلك
ن ( ن -2)
Solution .
n² + n(n−1) + n(n−2) + … + n(1)
Step 1: Factor out n
n·n + n(n−1) + n(n−2) + … + n(1)
= n [ n + (n−1) + (n−2) + … + 1 ]
هذا المقدار عبارة مجموع الأعداد المتتالية
Step 2: Sum of first n natural numbers
n + (n−1) + (n−2) + … + 1
= n(n+1) / 2
Step 3: Substitute
= n × ( n(n+1) / 2 )
Step 4: Simplify
= n² (n+1) / 2
Step 5: Expand (optional)
= (n³ + n²) / 2
or
= ½ n³ + ½ n²
✅ Final Answer:
n^3 / 2 + n^2/ 2
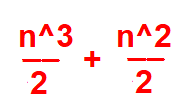
ويساوي
a_n = 0.5 n^3 + 0.5 n^2
=========================================================================================
هناك من ينظر الى الشكل بنظرة متأملة ويقترح قانون الحد العام
الشكل الثالث
بالنظر الى الشكل من الأعلى الى الأسفل ويعد المكعبات يجدها
1(3) +2(3)+3(3)
1ن+2ن+3ن +.......
ن ( 1+2+3+.........)
ن في مجموع ( 1+2+3+.........)
مجموع ( 1+2+3+.........)
يساوي
وعليه الحد العام
ن ضرب المقدار ويساوي
وبعد التبسيط يصبح المقدار
ويساوي
a_n = 0.5 n^3 + 0.5 n^2
=========================================================================================
نظرة مختلفة
=========================================================================================
طريقة الفروق
حدود المتتالية
1, 6, 18, 40, 75,
الحد القيمة ف1 ف2 ف3 1 1 5 7 3 2 6 3 18 12 4 40 22 10 5 75 35 13 ن ؟
الخطوة 1: التحقق من درجة المتتالية باستخدام الفروق
1, 6, 18, 40,75
الفرق الاول
5, 12, 22, 35
الفرق الثاني
7, 10, 13
الفرق الثالث
3
الفرق الثالث ثابتومقداره يساوي 3
المتتالية من الدرجة الثالثة.
الخطوة 2: الصيغة العامة للمتتالية
a n^3 + b n^2 + c n +d
1, 6, 18, 40, 75,
الجدول
125a+25b+5c+d
64a+16b+4c+d
27a+9b+3c +d
8a+4b+2c+d
a+b+c+d
d1 61a+9b+c 37a+7b+c 19a+5b+c 7a+3b+c d2 24a+2b 18a+2b 12a+2b d3 6a
الحد القيمة ف1 ف2 ف3 1 1 5 7 3 2 6 3 18 12 4 40 22 10 5 75 35 13 ن ؟
6a = 3
12a+2b=7
7a+3b+c=5
a+b+c+d=1
1, 6, 18, 40, 75,
الخطوة 3: استخدام 4 حدود لحل النظام
التعويض بواحد والمساواة بالحد الاول = 1
a + b + c + d = 1
التعويض ب ٢ والمساواة بالحد الثاني = 6
8a + 4b + 2c + d = 6
الفرق بينهما
7a + 3b + c = 5
التعويض بثلاثة والمساواة بالحد الثالث =18
27a + 9b + 3c + d = 18
التعويض ب ٤ والمساواة بالحد الرابع= 40
64a + 16b + 4c + d = 40
بالطرح
(2)−(1):
الفرق بينهما
7a + 3b + c = 5
معادلة رقم
(5)
بالطرح
(3)−(2):
19a + 5b + c = 12
معادلة رقم
(6)
بالطرح
(4)−(3)
37a + 7b+ c = 22
معادلة رقم
(7)
(6)−(5)
الفرق بينهم12a + 2b = 7
معادلة رقم
(8)
(7)−(6)
18a + 2b = 10
معادلة رقم
(9)
(9)−(8)
الفرق بينهم
الفرق الثالث في التعويض= الفرق الثالث في المتتالية
6a = 3
نحصل على
a = 0.5
من (8):
12(0.5) + 2b= 7
يعني
6 + 2b = 7
ومنها
B = 0.5
من (5):
7(0.5) + 3(0.5) + c = 5
3.5 + 1.5 + c = 5
c = 0
من (1):
0.5 + 0.5 + 0 + d = 1
d = 0
الخطوة 4: الصيغة العامة
a = 0.5
B = 0.5
a_n = 0.5 n^3 + 0.5 n^2
==================================================
بعض البرمجيات من الممكن الوصول للقاعدة من مجرد النظر
عدد مربعات هذا الشكل يتبع قانون مجموع الأعداد المتتالية
وبالطريقة نفسها لو كانت مكعبات
الحد الخامس من 1 الى 5
الحد الرابع من 1 الى 4
في المتتالية
وحيث ان الشكل مكرر ن مرة فيكون المجموع تكرار المجموع السابق ن مرة
a_n = 0.5 n^3 + 0.5 n^2
==================================================================================
1 + 3 + 5+7
قانون مجموع الأعداد الفردية
--------------------------------------------------------
|
الشكل 1 |
1 | 2 | 3 | ن |
|
|
|
|
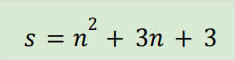
واضح أن جميع الأشكال تحتوي على ثلاث مربعات في الطبقة السفية

كما ان قلب كل شكل هو المستطيل المبني فوق المربعات السفلية
في الشكل الأول مستطيل 1 في 3

في الشكل الثاني مستطيل 2 في 4

في الشكل الثالث مستطيل 3 في 5

وفوقه المربعات 1 و 2 و3
وهي تمثل ن

الوسط ( القلب)
فيها مستطيل بعداه
ن(ن+2)
الصورة العامة للمتتالية
ن(ن+2) + ن +3
بالتبسيط
ن2+3ن+3
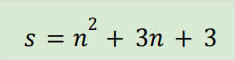
__________________________________________________
وبالنظر المتأمل في معظم المتتاليات يمكن الوصول الى القاعدة
مثال

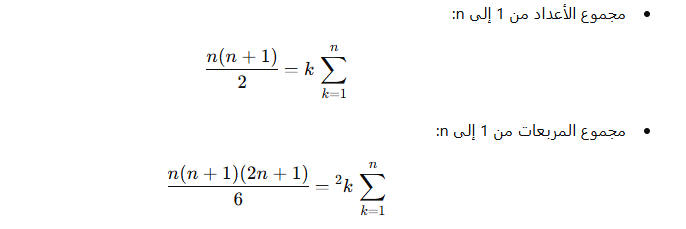

=========================================================
مثال


==============================================================

==========================================
**أنشطة حول المتتاليات **