بعض الأوامر على برمجية الجيوجبرا :
يمكن استخدام بعض الأوامر على البرمجية من خلال كتابة هذه الأوامر في حقل الأوامرثم Enter فيتحقق الأمر مباشرة على لوحة الرسم .
( مع ملاحظة أهمية وجود المؤشر في نهاية حقل الأوامر قبل اختيار Enter )
وهذه الأوامر كالتالي :
| م | الاستخدام | الأمر المناسب |
| 1 | حساب مجموع زوايا المثلث : |
"مجموع
زوايا المثلث " + " = " + (γ + α + β) |
| 2 | محيط المثلث : |
"محيط المثلث " + " = " + perimeterpoly1 |
| 3 | مساحة المثلث : |
" مساحة المثلث" + " = " + poly1 |
| 4 | مجموع ضلعين في مثلث : |
الطريقة الأولى : نطرح أحد الأضلاع من المحيط كالتالي: "a+b" + " = " + (perimeterpoly1 - c) الطريقة الثانية : مباشرة كالتالي مجموع ضلعين "a+c" + " =" + (a + c) |
| 5 | مجموع زاويتين في مثلث : |
"مجموع زاويتين في المثلث " + " = " + (γ + α) |
| 6 | مجموع زاويتين داخليتين في مثلث : |
" مجموع الزاويتين الداخليتين= " + (Angle[C, A, B] + Angle[B, C, A]) |
| 7 | قياس الزاوية الخارجية في مثلث : | " قياس الزاوية الخارجية = " + (Angle[D, B, A]) |
| 8 | أمر إظهار قيمة الزاوية |
" A قيمة الزاوية = " + (Angle[C, A, B]) |
| 9 | مربع طول ضلع : |
" مربع طول الضلع= " + (a²) |
| 10 | حاصل ضرب مسقطي الضلعين القائمين على الوتر |
+ "=حاصل ضرب مسقطي الضلعين القائمين على الوتر "Distance[A, B]*Distance[E, B[ |
| 11 |
معادة الخط المستقيم |
y = a x + b حيث : a= الميل ، b=الجزء المقطوع من الصادات. |
| 12 | معادلة الدائرة : |
(x-m)^2 + (y-n)^2=r^2 أو (x-m)2 + (y-n)2=r2 حيث إحداثا المركز ( m , n) , ونصف القطر r |
| 13 | دالة الجيب جا |
sin(x) |
| 14 | دالة جيب التمام جتا |
cos(x) |
| 15 | دالة الظل ظا |
tan(x) |
طريقة الاستخدام :
1- نسخ الأمر من الجدول باستخدام نسخ أو Ctrl+C .
2- الذهاب إلى حقل الأوامرواللصق باختيار لصق أو Ctrl+V .
3- اختيار Enter بعد التأكد من وجود المؤشر في نهاية حقل الأوامر.
وفيما يلي أمثلة وتطبيقات على الأوامر السابقة :
1- حساب مجموع زوايا المثلث :
يتم حساب مجموع زوايا المثلث بكتابة الأمر التالي في حقل المدخلات والأوامر:
"مجموع
زوايا المثلث " + " = " + (γ + α + β)
ثم إدخال Enter .
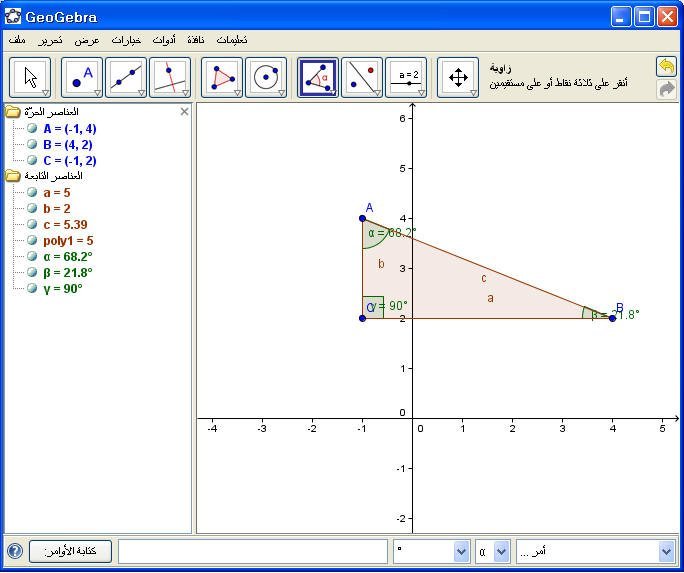
مثال : على الشكل المقابل أوجد مجموع زوايا المثلث :

الحل :
يتم حساب مجموع زوايا المثلث بكتابة الأمر التالي في حقل المدخلات والأوامر:
"مجموع
زوايا المثلث " + " = " + (γ + α + β)
كما في الشكل التالي
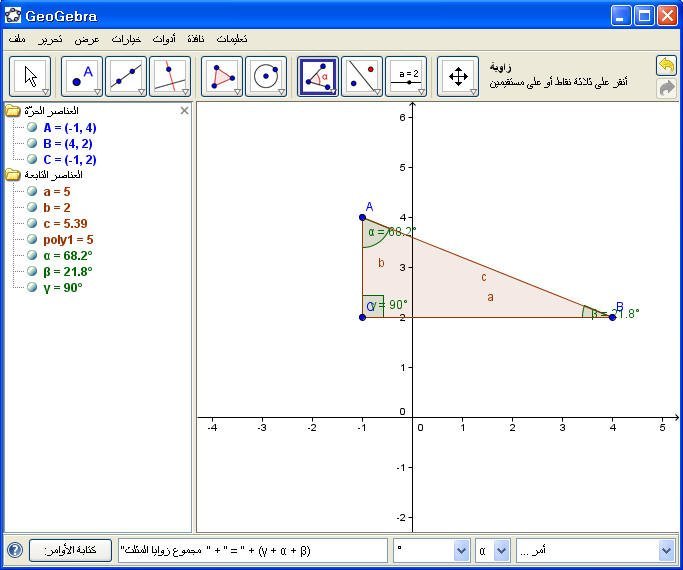
ثم Enter مع ملاحظة أن يكون المؤشر في نهاية كتابة الأمر في حقل المدخلات فيظهر المجموع كما يلي:
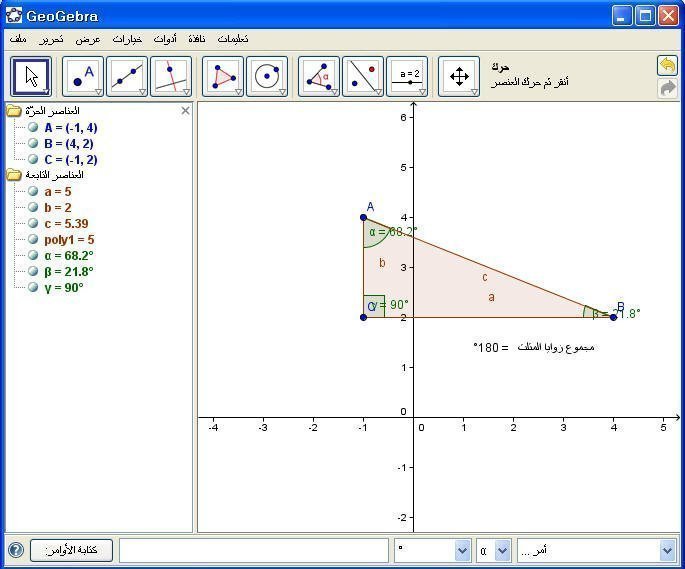
2- محيط المثلث :
"محيط المثلث " + " = " + perimeterpoly1
ثم Enter.
مثال2 : أوجد محيط المثلث السابق .
الحل :
نكتب في حقل الأوامرالأمر التالي :
"محيط المثلث " + " = " + perimeterpoly1
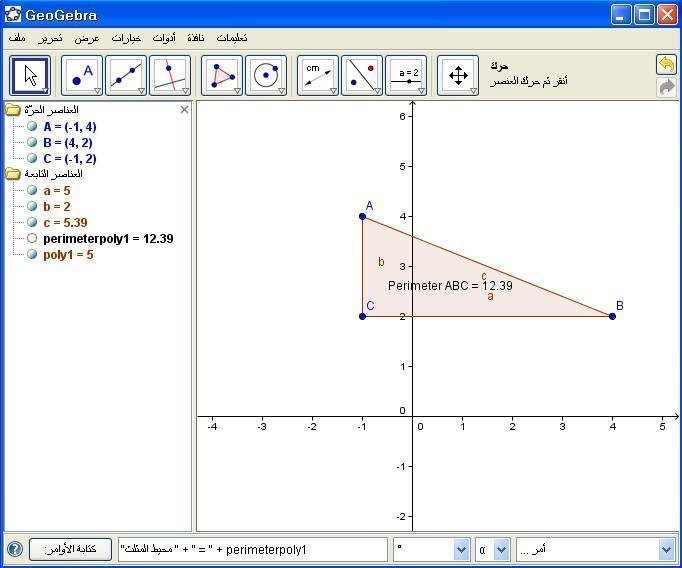
ثم Enter .
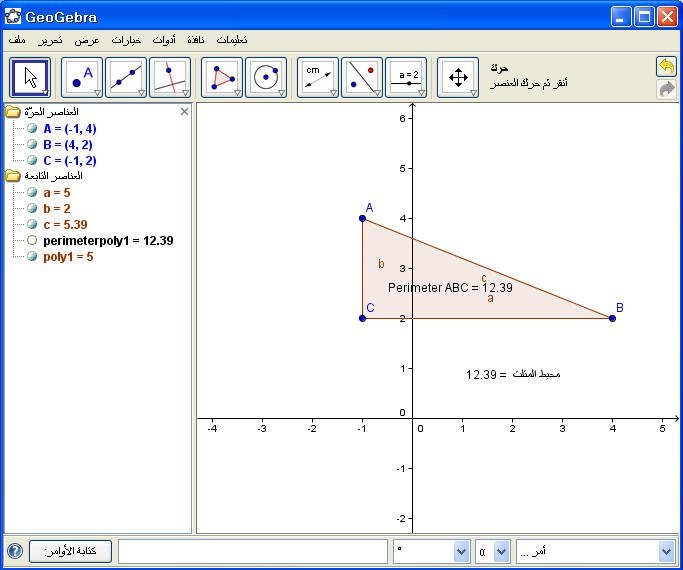
3- مساحة المثلث :
نكتب في حقل الأوامرالأمر التالي :
" مساحة المثلث" + " = " + poly1
ثم Enter .
مثال 3: في المثلث السابق أوجد مساحته .
الحل :
نكتب في حقل الأوامرالأمر التالي :
" مساحة المثلث" + " = " + poly1
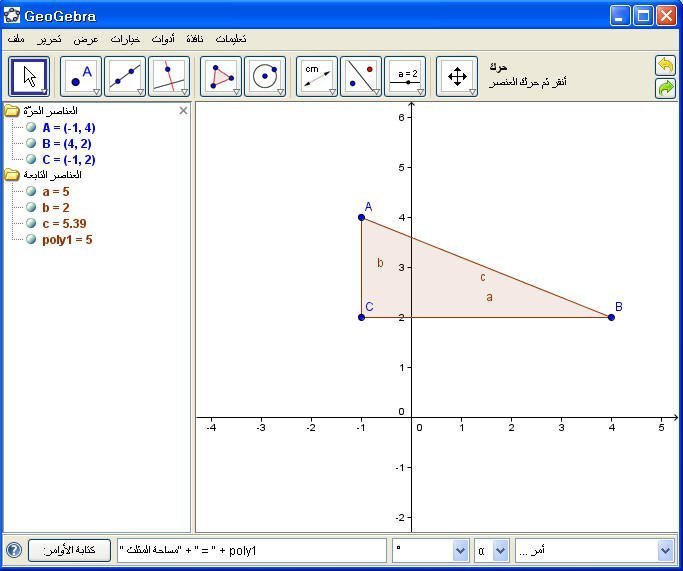
ثم Enter .
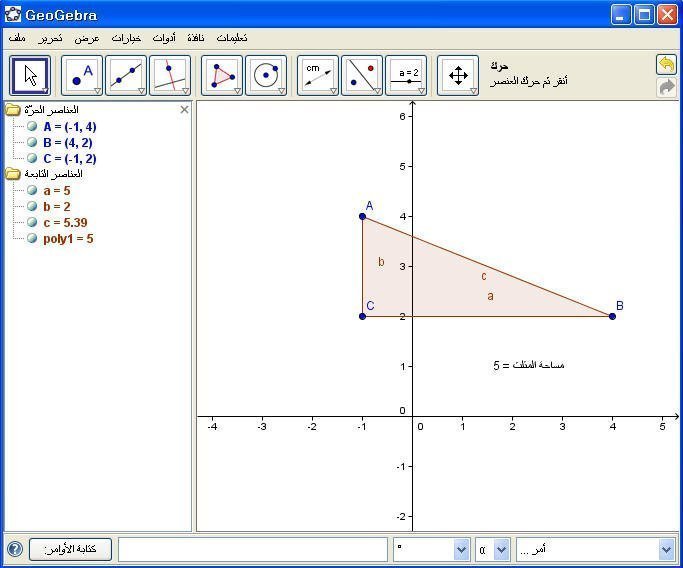
4- مجموع ضلعين في مثلث :
يمكن حساب مجموع ضلعين في مثلث بطريقتين :
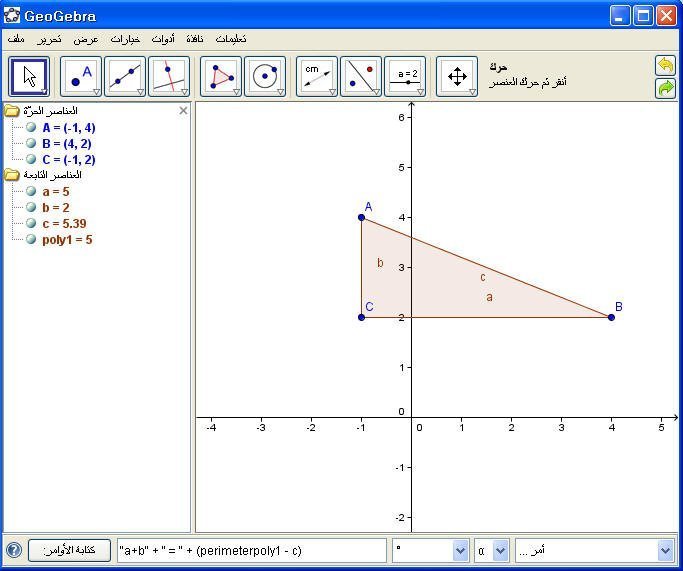
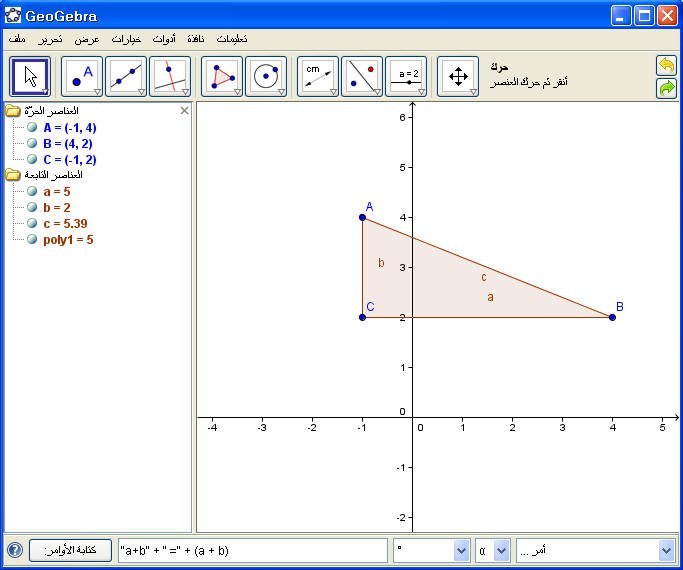
الأولى : نطرح أحد الأضلاع من المحيط كالتالي:
"a+b" + " = " + (perimeterpoly1 - c)
الطريقة الثانية : مباشرة كالتالي مجموع ضلعين
"a+c" + " =" + (a + c)
مثال : في المثلث السابق احسب مجموع ضلعين a , b :
الحل :
الطريقة الأولى :
الأولى : نطرح أحد الأضلاع من المحيط كالتالي:
"a+b" + " = " + (perimeterpoly1 - c)
ثم Enter.
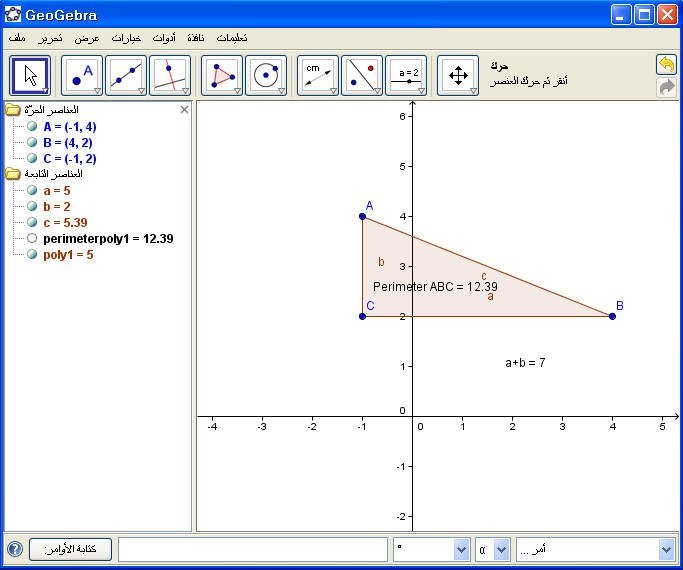
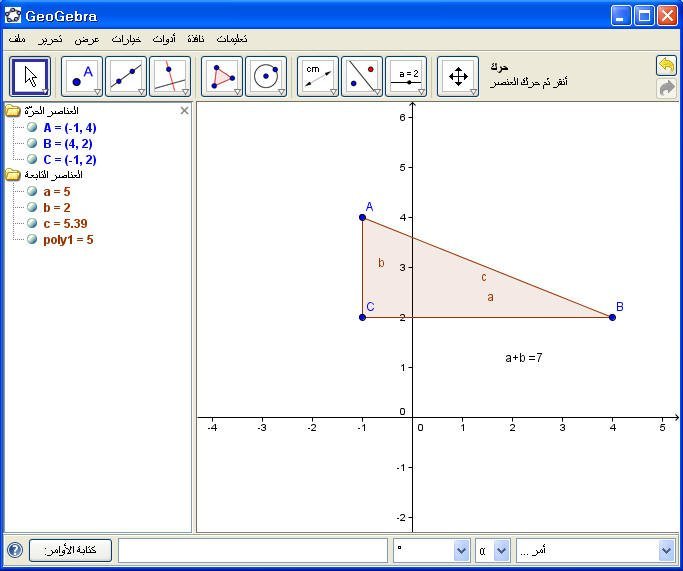
الطريقة الثانية :مباشرة بكتابة الأمر التالي :
"a+b" + " =" + (a + b)
ثم Enter .
5- مجموع زاويتين في مثلث :
"مجموع زاويتين في المثلث " + " = " + (γ + α)
مثال : في المثلث السابق أوجد مجموع زاويتين في المثلث .
الحل :
نكتب في حقل الأوامرلأمر التالي :
"مجموع زاويتين في المثلث " + " = " + (γ + α)
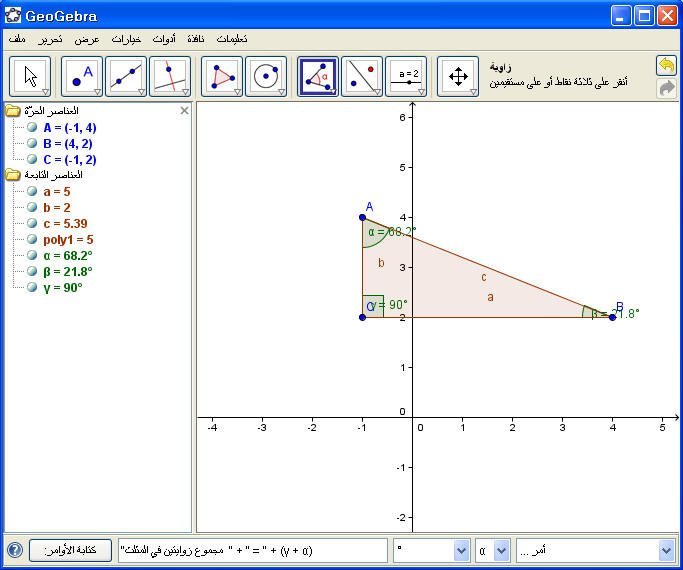
ثم Enter .
6- مجموع زاويتين داخليتين في مثلث :
" مجموع الزاويتين الداخليتين= " + (Angle[C, A, B] + Angle[B, C, A])
مثال : أوجد مجموع الزاويتين الداخليتين في المثلث السابق .
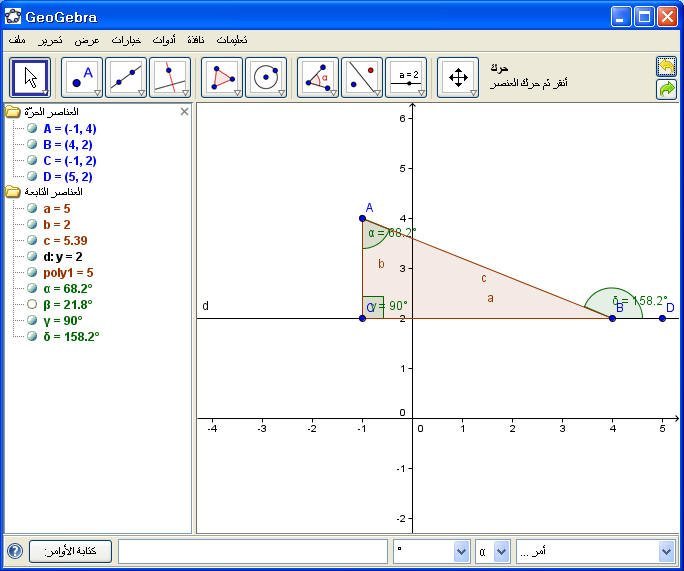
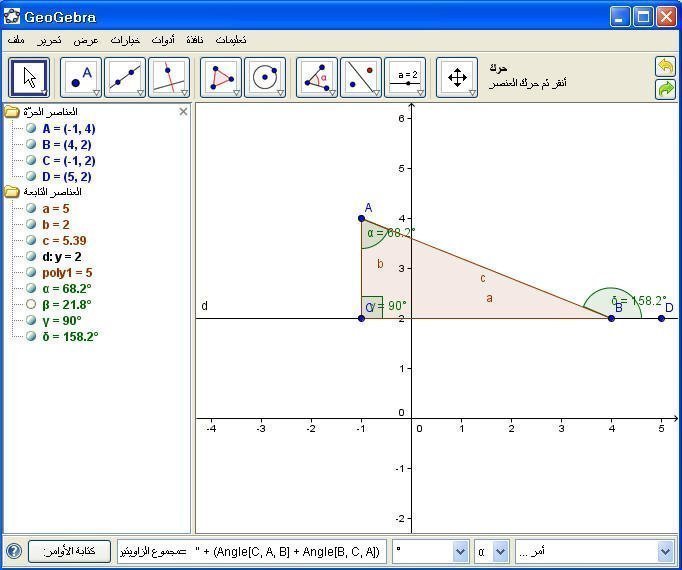
ثم Enter .
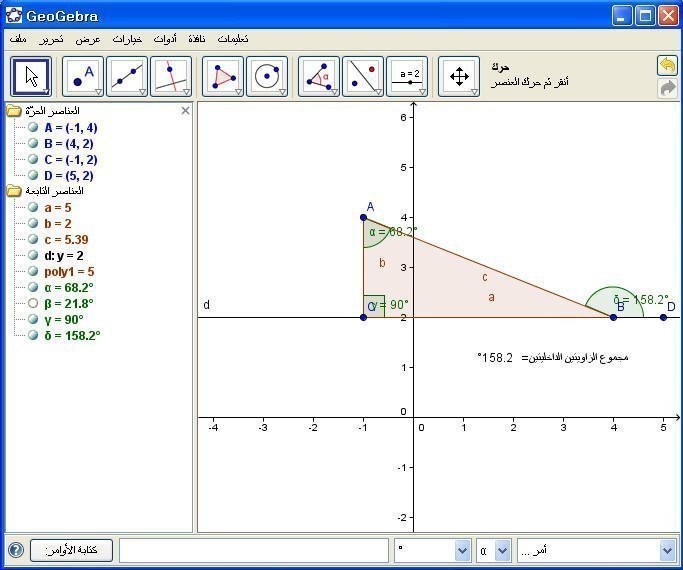
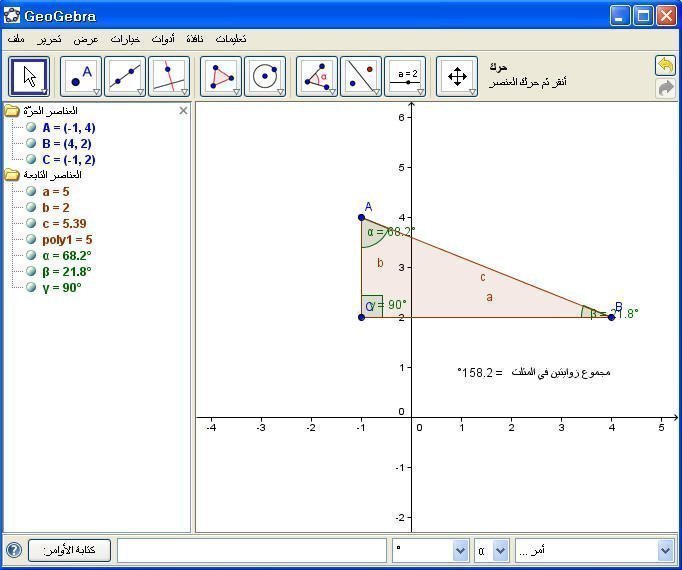
ويمكن ملاحظة قياس الزاوية الخارجية في المثلث ومقارنته مع مجموع الزاويتين الداخليتين .
مجموع الزاويتين الداخليتين = قياس الزاوية الخارجية .
7- قياس الزاوية الخارجية =
" قياس الزاوية الخارجية = " + (Angle[D, B, A])
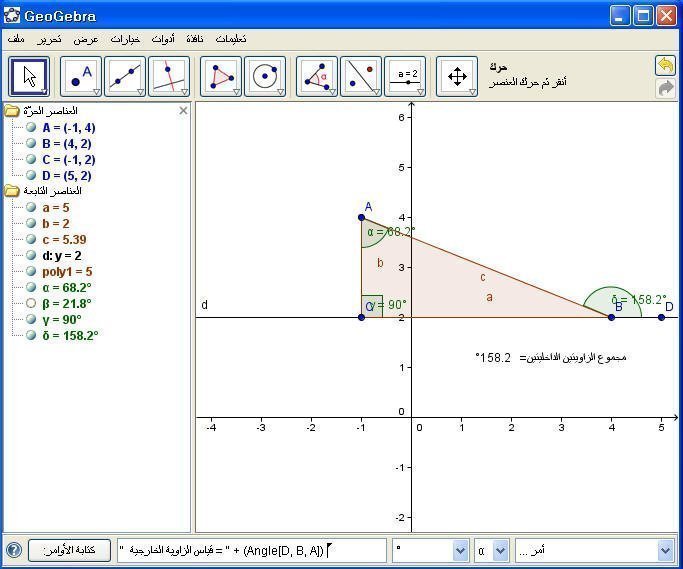
ثم Enter .
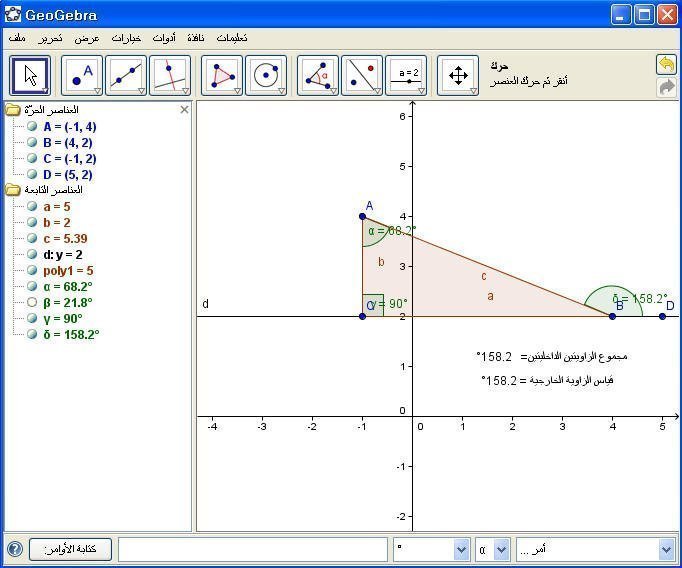
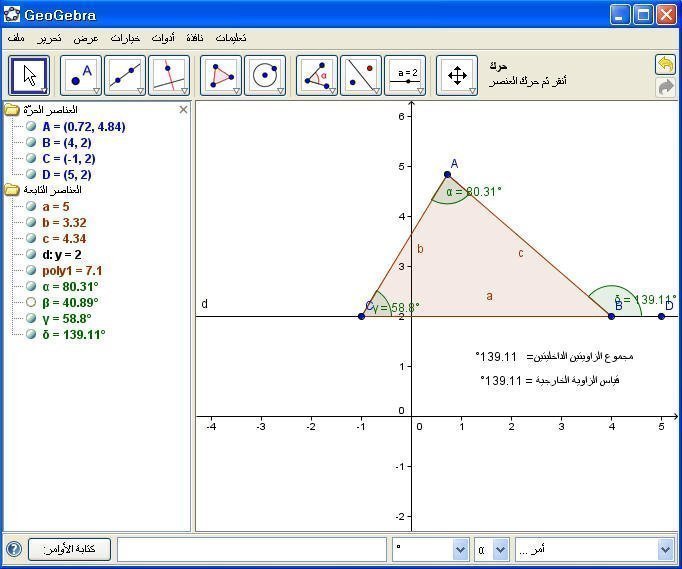
وهنا نلاحظ عند تغيير قياس الزاويتين الداخليتين تتغير تبعاً لها قياس الزاوية الخارجية كما يلي :
8- مربع طول ضلع :
يمكن حساب مربع ضلع باستخدام الأمر التالي :
" مربع طول الضلع= " + (a²)
مثال : احسب مربع الضلع a في المثلث السابق .
الحل :
نكتب في حقل الأوامرلأمر التالي :
" مربع طول الضلع= " + (a²)
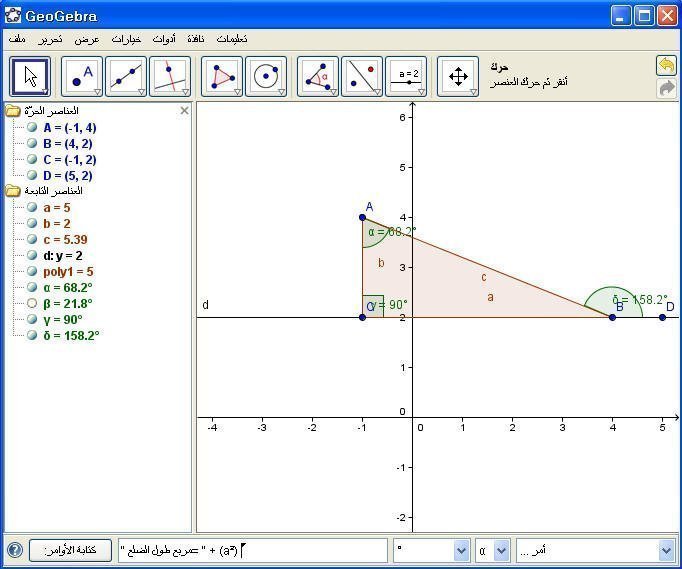
ثم Enter .
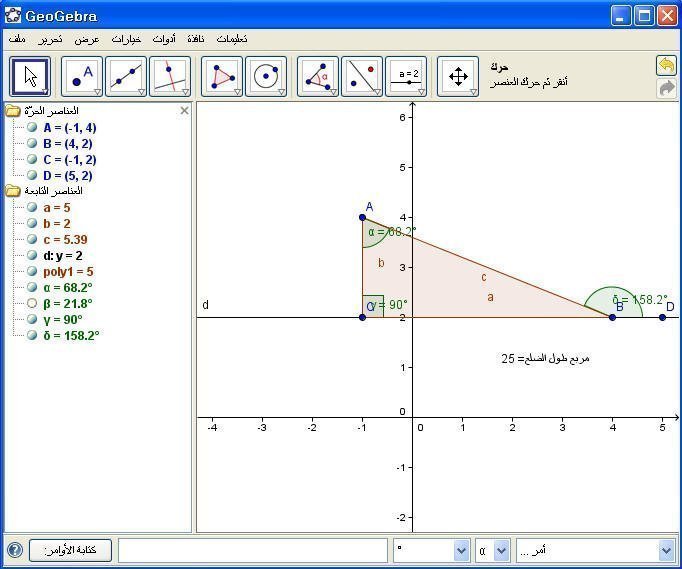
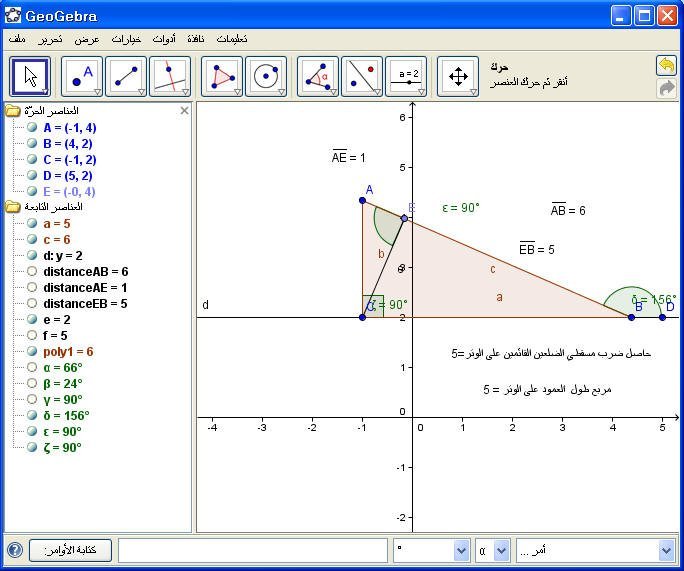
9- العمود الساقط من القائمة على الوتر = حاصل ضرب مسقطي المائلتين على الوتر .
مثال : على الشكل السابق
نوجد مربع العمود النازل على الوتر من خلال الأمر
" مربع طول الضلع= " + (a²)
وحيث العمود اسمه e نستخدم الأمر
" مربع طول العمود على الوتر " + (e²)
فينتج :
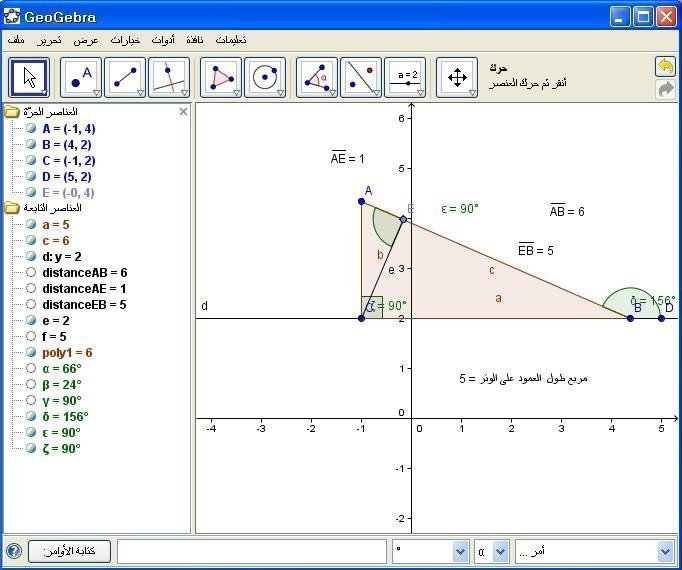
ثم نوجد حاصل ضرب مسقطي الضلعين القائمين على الوتر بالأمر كالتالي :
+ "=حاصل ضرب مسقطي الضلعين القائمين على الوتر "Distance[A, B]*Distance[E, B[
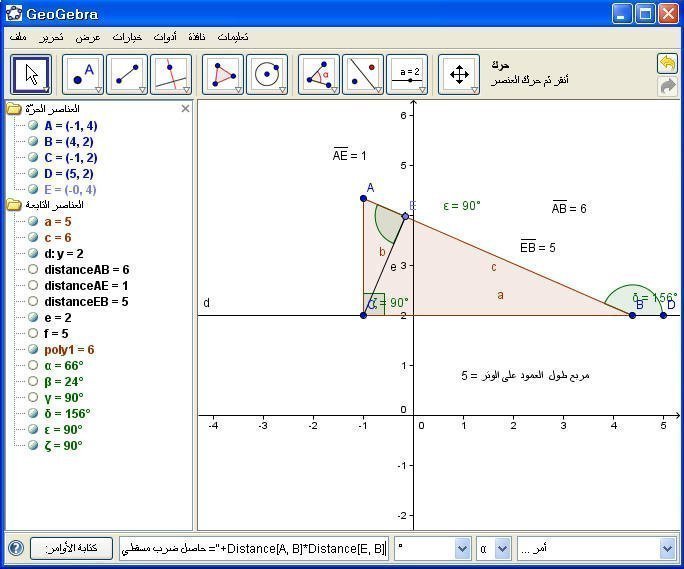
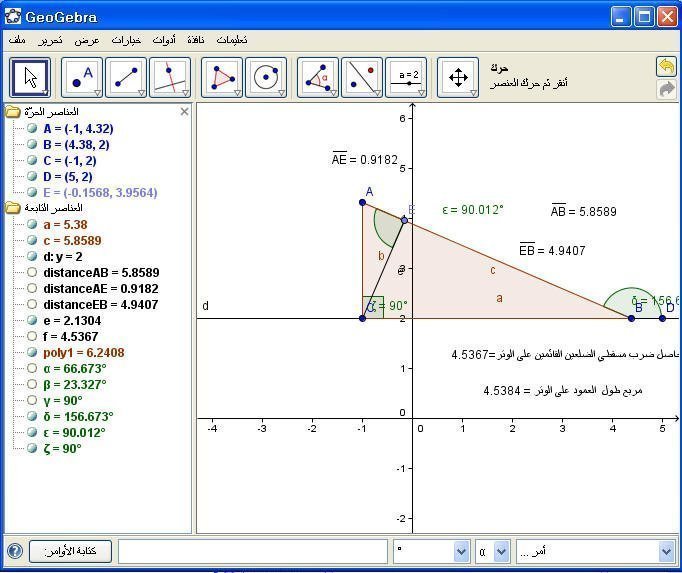
ويمكن الدقة في ذلك من خلال تغيير الأجزاء العشرية إلى 3 أرقام كالتالي :
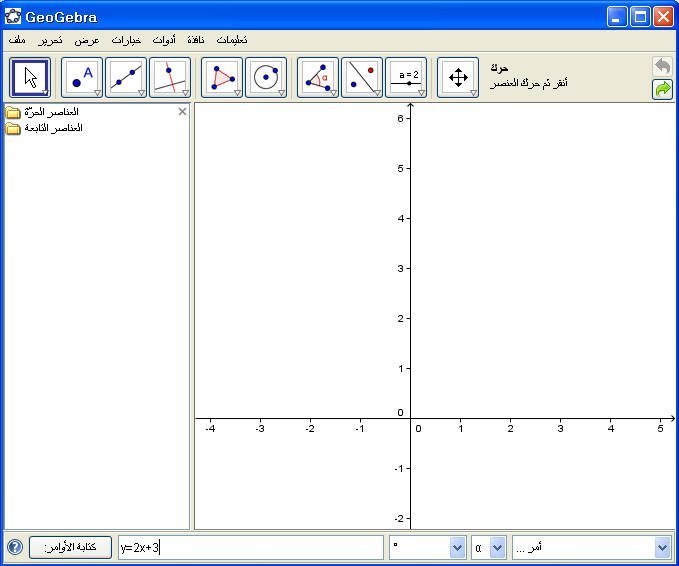
10- معادلة الخط المستقيم :
y = a x + b
مثال : مثل الخط المستقيم y = 2x +3
الحل :
نكتب في حقل الأوامر المعادلة y = 2x +3
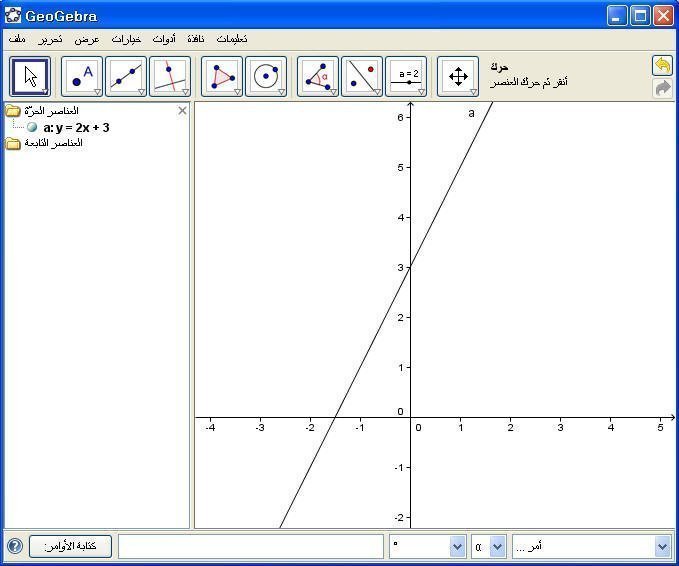
ثم Enter .
11- معادلة الدائرة :
(x-m)2 + (y-n)2=r2
أو
(x-m)^2 + (y-n)^2=r^2
حيث المركز هو ( m ، n) و نصف القطر هو r .
مثال : مثل الدائرة التي مركزها ( 2 ، 1) ونصف قطرها = 3 .
الحل :
نكتب المعادلة التالية وفقاً للمركز ونصف القطر في حقل الأوامر:
(x-2)2 + (y-1)2=32
أو المعادلة :
(x-2)^2 + (y-1)^2=3^2
كالتالي
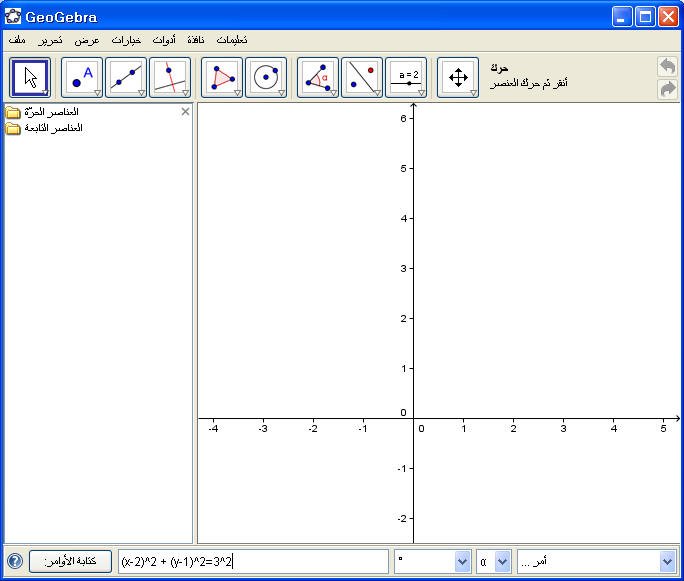
ثم Enter .
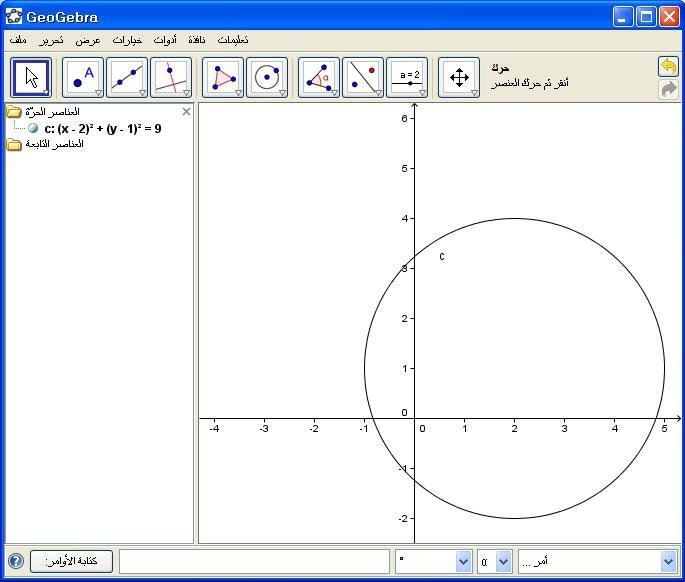
12- دالة الجيب حا :
يمكن إدخال الأمر( sin (x مباشرة في حقل الأوامر ثم Enter فينتج شكل الدالة :
مثال :
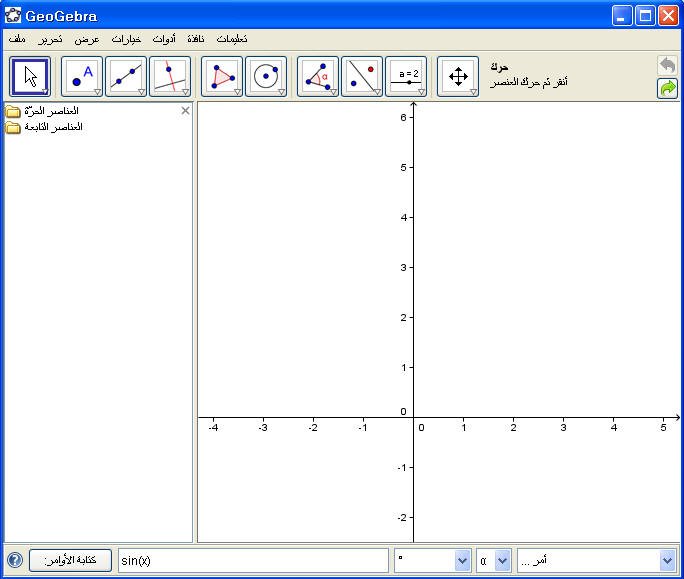
ثم Enter
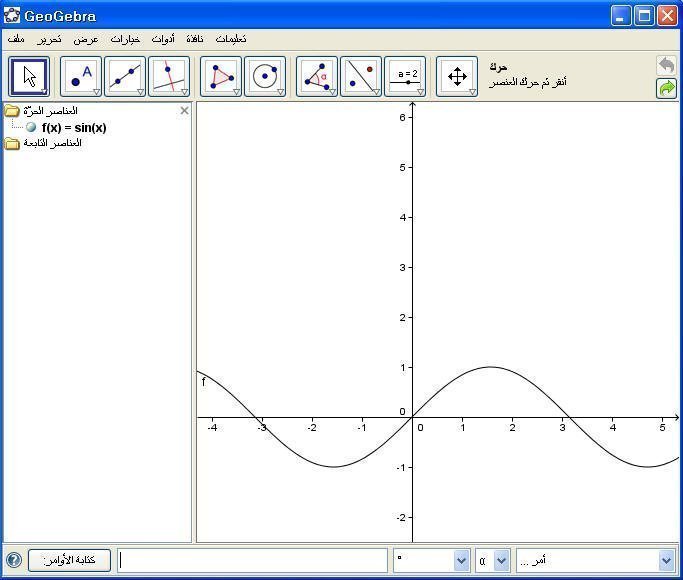
13- دالة جيب التمام جتا :
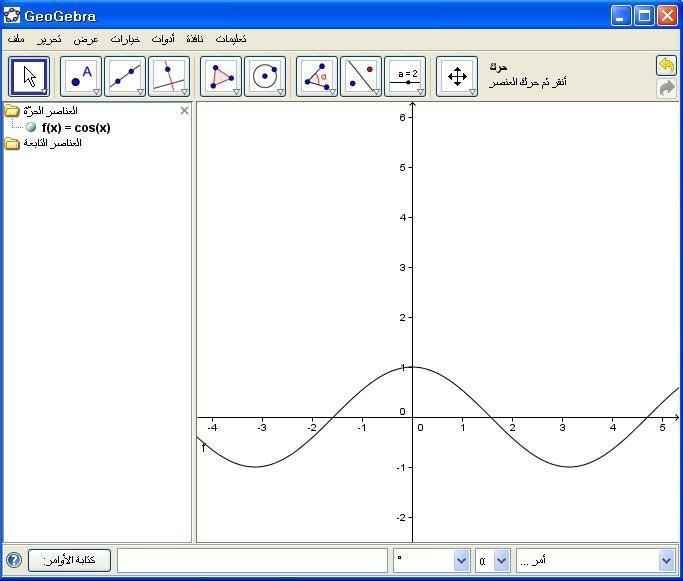
يمكن إدخال الأمر( cos (x مباشرة في حقل الأوامر ثم Enter فينتج شكل الدالة :
مثال :
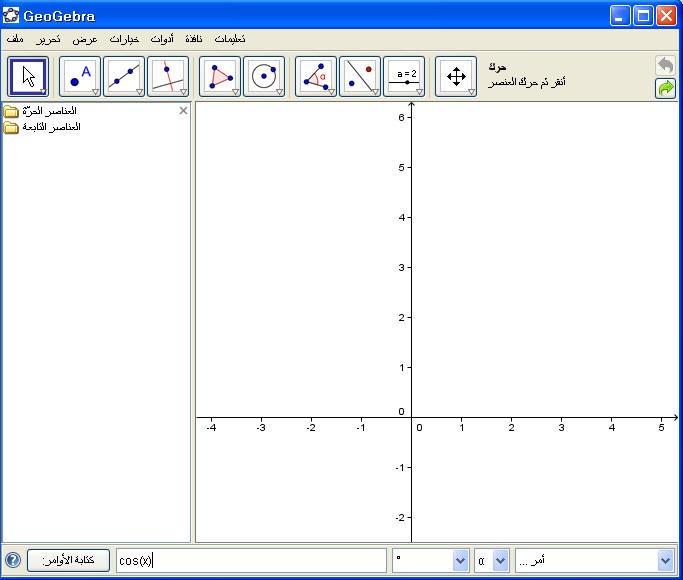
ثم Enter ..
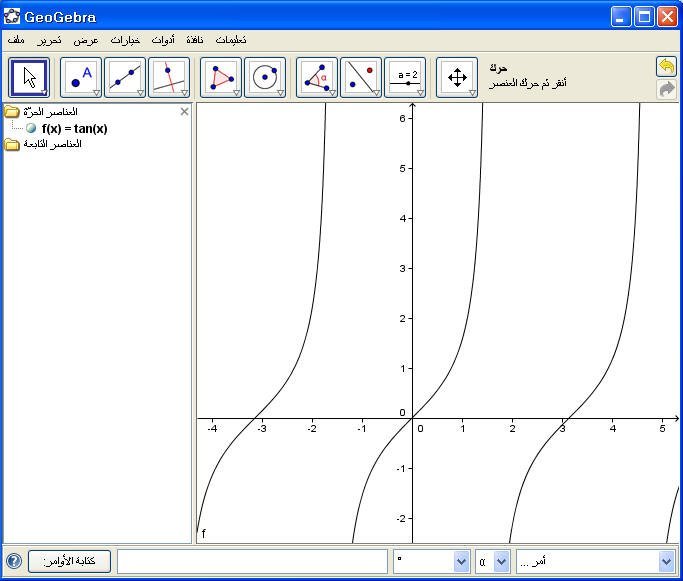
14- دالة الظل ظا :
يمكن إدخال الأمر( tan (x مباشرة في حقل الأوامر ثم Enter فينتج شكل الدالة :
مثال :
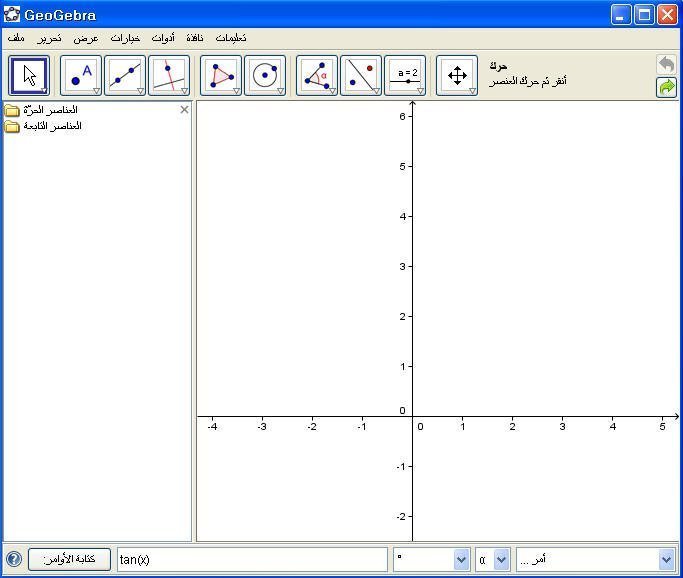
ثم Enter ...فينتج :