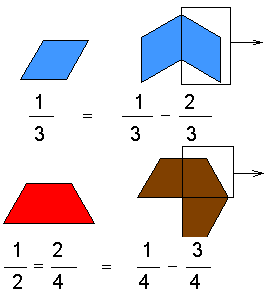
طرح الكسور
1-طرح كسرين لهما مقام مشترك:
نوضح للطالب أولاً إن عملية طرح كسرين لهما مقام مشترك هي عملية عكسية لعملية جمع كسرين لهما مقام مشترك ثم نترك له المجال ليجرب ذلك بنفسه
مثال:

نلاحظ من ذلك أنه عند طرح كسرين لهما مقام مشترك نقوم بطرح البسط من البسط ويبقى المقام المشترك
ثم يستنتج أن:
2- طرح كسرين اعتياديين:
أولاً نترك للطالب المجال حساب الفرق بين كسرين ملموسين بقطع النماذج بحيث يمكنه الحصول من أحدها على الآخر ثم نكمل بعد ذلك بكسور مختلفة
مثال(1):
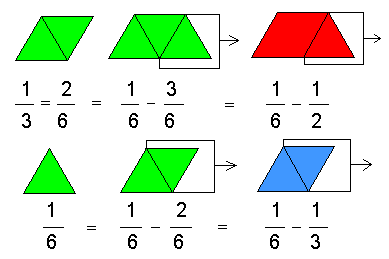
نلاحظ هنا في المرة الأولى جزأنا النصف إلى ثلاثة أسداس ثم سحبنا السدس منها ليبقى لدينا سدسين أي ثلث أما المرة الثانية جزأنا الثلث إلى سدسين ثم سحبنا السدس ليبقى السدس، كما نلاحظ هنا أننا استطعنا تجزئة الكسر الأول إلى أجزاء من الكسر الثاني.
الآن إذا أُعطي الطالب كسرين لا يمكنه تمثيلها بقطع النماذج بحيث لا يمكنه الحصول من أحدها على الآخر سنرشده لإتباع الآتي:
* أوجد كسراً مكافئاً للكسر الأول.
* أوجد كسراً مكافئاً للكسر الثاني.
* أطرح الكسران الحاصلان واللذان لهما مقام مشترك.
وسنترك له المجال ليجرب بنفسه
مثال(2):
لإتمام عملية الطرح التالية سيتبع ما يلي:
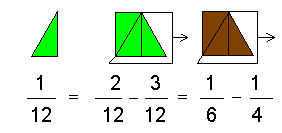
نلاحظ هنا أننا حولنا الكسرين كلاهما إلى كسرين آخرين مكافئين لهما ثم تممنا عملية الطرح
ومع التكرار نستنتج
ولكي نستنتج قاعدة عامة لعملية الطرح سنتابع الخطوات التالية
نفرض أن ![]() ،
، ![]()
بالتالي ب × م = أ ، د × ن = جـ وبالضرب في د ، ب نحصل على د ( ب × م ) = د أ ، ب ( د × ن ) = ب جـ
وحيث أن الضرب إبدالي وتجميعي فإن
( د ب ) م = د أ ، ( د ب ) ن = ب جـ
وبطرح الحدين
( د ب ) م – ( د ب ) ن = د أ – ب جـ
إذن
( د ب ) ( م – ن ) = د أ – ب جـ
وعليه فإن ![]()
وعموماً

تقويم:
أنجز عامل ![]() عمله
في اليوم الأول،و
عمله
في اليوم الأول،و ![]() عمله
في اليوم الثاني،و
عمله
في اليوم الثاني،و ![]() العمل
في اليوم الثالث.
العمل
في اليوم الثالث.
* ما هو الكسر الذي يمثل العمل الذي أنجزه ؟
* ما هو الكسر الذي يمثل الباقي من العمل ؟