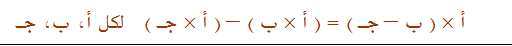خصائص عملية الضرب
أ - الإبدال
سبق وأن مثل الطالب حاصل ضرب العددين 3 ×4 = 12

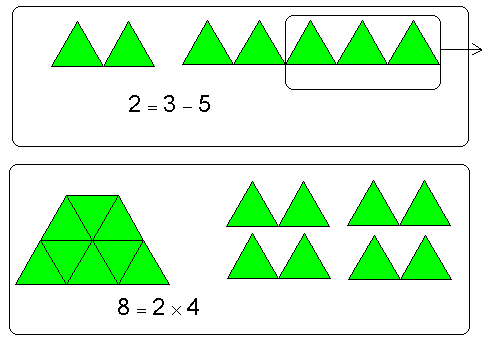
الآن إذا غيرنا مكان العددين بحيث يصبح كالتالي 4 × 3 نطلب من الطالب أن يمثلها بقطع النماذج ليدرك بنفسه الناتج كالتالي:

وفي كلا الحالتين سيجد أن النتيجة هي نفسها ولم تتغير بذلك ومع تكرار الأمثلة يستنتج الطالب أنه في عملية الضرب لاتتغير النتيجة بتغير أماكن العددين وعموماً
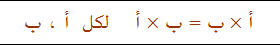
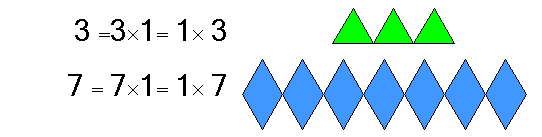
ب - العنصر المحايد
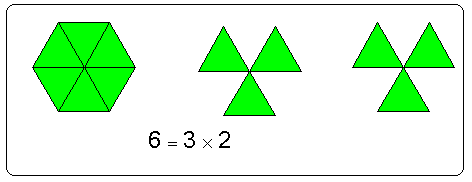
عرفنا سابقاً أن العنصر المحايد هو العدد الذي لا يؤثر ولا يغير في أي عدد آخر فعندما نكرر العدد 3 مرة واحدة يبقى كما هو 3 ، كذلك إذا كررنا العدد 7 مرة واحدة يبقى كما هو 7 كالتالي:
وعموماً
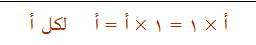
ج - التجميع
مثال:
في البداية سنضرب 2 × 3 ثم نأخذ الناتج لنضربه في 4 ونترك الطالب يجرب بقطع النماذج ما هي النتيجة ؟
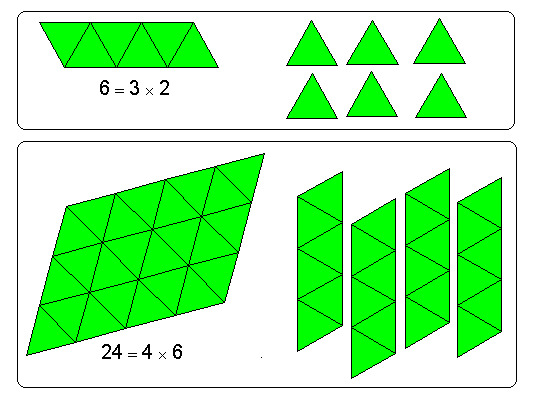
الآن نغير الأعداد سنضرب أولا ًالعددين 3 × 4 ؟
ثم نضرب العدد 2 في النتيجة ونطلب منه يجرب ذلك بواسطة قطع النماذج كالتالي
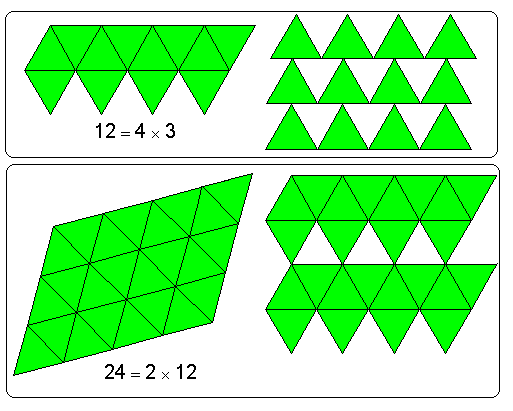
سيرى في الحالتين السابقتين أنه حصل على نفس النتيجة وهذه الخاصية هي خاصية التجميع ومع تكرار المحاولات من الطالب بقطع النماذج على هذه الخاصية يستطيع إدراكها بشكل ملموس مما يؤدي إلى تثبيتها في ذهنه وعموماً

د - توزيع التجميع على الضرب
مثال(1):
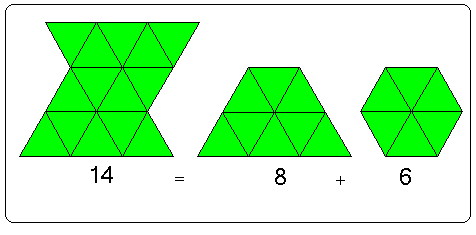
سنحاول إيجاد حاصل ضرب 2 × ( 3 + 4 )
أولاً ندع الطالب يحاول إيجاد المجموع ( 3 + 4 ) وبعد إيجاده للمجموع يقوم بضربه في 2 ثم يرى النتيجة المتوقعة ويتضح ذلك من الشكل التالي
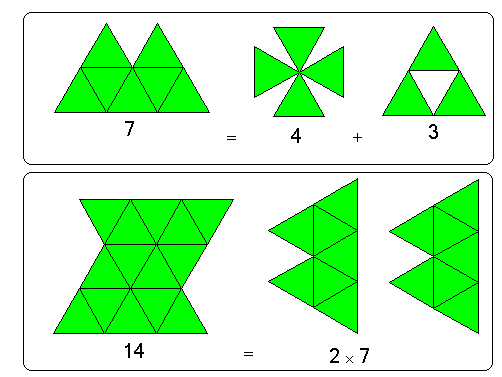
مثال(2):
هنا سنحاول إيجاد ( 2 × 3 ) + ( 2 × 4 )
أولاً : نترك الطالب يجد حاصل الضرب (2 × 3 )
ثانياً: نترك الطالب يجد حاصل الضرب ( 2 × 4 )
ثالثاً: نترك الطالب يجد مجموع العمليتين السابقتين
أولاً
ثانيا
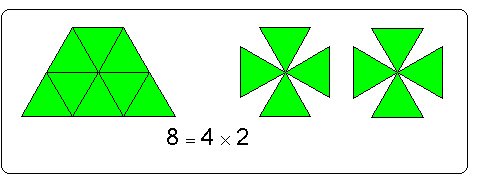
ثالثا
جمع النتيجتين من اولا مع ثانيا
ثم نترك الطالب ليقارن بين النتيجتين في المثالين السابقين سيجد أنهما متساويتين وبذلك يستنتج أن
2 × ( 3 + 4 ) = ( 2 × 3 ) + ( 2 × 4 )
2 × 7 = 6 + 8
14 = 14
قبل تعميم النتيجة السابقة نترك الطالب يحاول تكرارها مع أعداد أخرى وبعد ذلك نسمي هذه الخاصية بخاصية توزيع الضرب على الجمع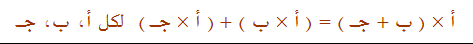
هـ - توزيع الضرب على الطرح
مثال(1):
أوجد العملية التالية 4 × ( 5 – 3 )
أولاً نترك الطالب يحسب المقدار ( 5 – 3 ) ثم يضرب الناتج في 4
مثال(2):
أوجد العملية التالية (4 × 5 ) – ( 4 × 3 )
أولاً : سيجد المقدار ( 4 × 5 )
ثانياً: سيجد المقدار ( 4 × 3 )
ثالثاً: سيجد الفرق بين المقداريناولا :
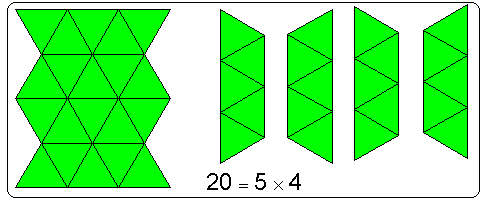
ثانيا :
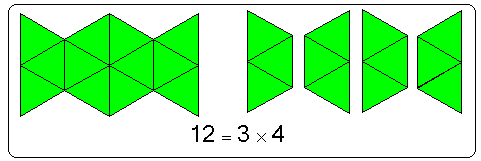
ثالثا
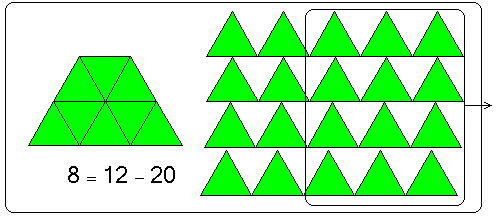
بعد المقارنة يستنتج : 4 × ( 5 – 3 ) = ( 4 × 5 ) – ( 4 × 3 )
4 × 2 = 20 - 12
8 = 8
أي أن الضرب يتوزع على الطرح ومع تكرار الأمثلة نعمم النتيجة