( 3 – 4 ) التحليل بتمييز المتطابقة

محتويات التعلم :

                المهارات :

1-             تحليل كثيرة الحدود إلى عواملها الأولية بطريقة تمييز المتطابقة .

2-             تمييز العبارة الرياضية التي تمثل مربعاً كاملاً عن التي لا تمثل ذلك باستخدام القطع الجبرية .

الزمن اللازم للتدريس :

        حصتان .

الأهداف :

1-             أن يحلل الطالب كثيرة الحدود إلى عواملها الأولية بطريقة تميز المتطابقة .

2-             أن يميز الطالب بين العبارة الرياضية التي تمثل مربعاً كاملاً وتلك التي لا تمثل ذلك باستخدام القطع الجبرية .

الوسائل التعليمية :

القطع الجبرية – البطاقة الجبرية – السبورة – جهاز عرض الشفافيات – ورق العمل الخاصة بالمدرس.

التهيئة :

سبق في الدرس الماضي وأن أدرك الطلاب أن تحليل كثيرة الحدود يعنى كتابتها على صورة ضرب عواملها الأولية وفي هذا الدرس سيتعرف الطلاب على طريقة ثانية في التحليل .

العرض :

        يراجع المعلم مع الطلاب المتطابقات الأساسية التالية :

        ( س + ص )² = س² + 2 س ص + ص²

        ( س _ ص )² _ س² + 2 س ص + ص²

        (س _ ص ) ( س + ص ) = س² _ ص²

إذ أن معرفة صيغ المتطابقات تسهِّل عملية التحليل غير أنه من المهم أن نميز عبارة جبرية على أنها تمثِّل متطابقة أو لا تمثل وذلك عن طريق ملاحظة حدودها وفي هذا الدرس حالتين هما :

        ( 1 ) تحليل المربع الكامل .

        ( 2 ) تحليل الفرق بين مربعين .

أولاً :

تحليل المربع الكامل :

لقد سبق وأن تعرَّف الطلاب على متطابقة مربع مجموع حدين وكذا مربع الفرق بين حدين بصورة محسوسة باستخدام البطاقة والقطع الجبرية لكننا إذا أردنا أن نحلل كثيرة حدود بطريقة تمييز المتطابقة فلا يخلو الأمر هنا من حالتين :

        الحالة الأولى :

أن تكون كثيرة الحدود المعطاة ذات إشارة موجبة في جميع حدودها ففي هذه الحالة نقوم ببناء مربع كامل في الربع الموجب للبطاقة الجبرية فإذا تمكنا من ذلك فإن المقدار المعطى يمثل مربعاً كاملاً .

وبإكمال القطع المناسبة في المجرى الأفقي والرأسي للبطاقة نكون قد حللنا كثيرة الحدود المعطاة إلى عاملين ، والمثال التالي يوضح ذلك .

     مثال :

حلل المقدار س² + 6 س + 9 إلى عاملين إن أمكن باستخدام البطاقة والقطع الجبرية .

        الحل :

بما أن جميع حدود المقدار ذات إشارة موجبة فإننا نحاول أن نبني مربعاً كاملاً في الربع الأول للبطاقة يمثِّل المقدار المعطى كما في الشكل التالي :

سيلاحظ الطلاب أننا استطعنا بناء مربع كامل فهذا يعني أن المقدار المعطى يمثل مربعاً كاملاً وبإكمال القطع المناسبة في المجرى الأفقي والمجرى الرأسي للبطاقة نكون قد حللنا المقدار المعطى كما في الشكل التالي :

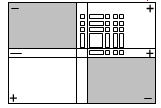
أي أن س² + 6 س + 9 = ( س + 3 ) ( س + 3 )  = ( س + 3 )²                وهو المطلوب .

نشاط :

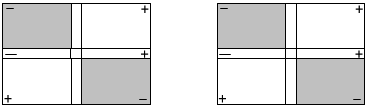
الحالة الثانية :

أن تكون كثيرة الحدود المعطاة ذات إشارة سالبة في حدها الأوسط ففي هذه الحالة نقوم بوضع القطع الجبرية لكل حد كما يلي :

-         القطع التي تمثل المقدار المربع توضع الربع الأول للبطاقة .

-         القطع التي تمثل الحد الأوسط توزع بالتساوي بين الربع الثاني والرابع للبطاقة .

-    القطع التي تمثل الحد الثالث نبني بها مربعاً في الربع الثالث للبطاقة ضلعه يكافئ القطع الموضوعة في الربع الثاني أو الرابع للبطاقة .

فإذا استطعنا فعل ذلك فإن المقدار المعطى يمثل مربعاً كاملاً وبإكمال القطع الجبرية المناسبة في المجرى الأفقي والرأسي للبطاقة نكون قد حللنا المقدار المعطى والمثال التالي يوضح ذلك .

       مثال :

حلل المقدار س² _ 4 س + 4 إلى عاملين إن أمكن باستخدام البطاقة والقطع الجبرية ؟

        الحل :

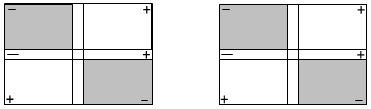
بما أن المقدار المعطى ذو إشارة سالبة في حده الأوسط فإننا نتبع الخطوات المذكورة سابقاً والشكل التالي يوضح ذلك :

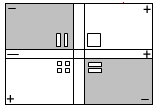
سيلاحظ الطلاب أننا استطعنا تطبيق الخطوات المطلوبة وبإكمال القطع المناسبة في المجرى الأفقي والرأسي للبطاقة قد حللنا المقدار كما في الشكل التالي :

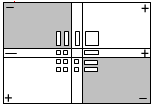
أي أن س² _ 4 س + 4 = ( س _ 2 ) ( س _ 2 )

                = ( س _ 2 )²

                وهو المطلوب .

       نشاط :

حلل المقدار س² _ 2 س + 1 إلى عاملين إن أمكن باستخدام البطاقة والقطع الجبرية .

ثانياً :

تحليل الفرق بين مربعين :

لقد سبق وأن تعرَّف الطلاب على متطابقة الفرق بين مربعين بصورة محسوسة باستخدام البطاقة والقطع الجبرية لكن إذا أردنا أن نحلل كثيرة الحدود بطريقة تمييز متطابقة الفرق بين مربعين فإننا نتبع الخطوات التالية:

1-      نضع القطع الجبرية التي تمثل الحد الأول في الربع الأول للبطاقة.

2-      نضع القطع الجبرية التي تمثل الحد الثاني في الربع الرابع للبطاقة.

3-  نقوم ببناء مربع طول ضلعه يمثل مجموع طولي القطع التي تمثل الحد الأول والثاني ( وذلك على افتراض عدم وجود محور أفقي يفصل بينهما ) وذلك بإضافة المقدار الصفري للربعين الأول والرابع .

4-  عند ذلك نضع القطع الجبرية المناسبة في المجرى الأفقي والرأسي للبطاقة فنكون قد حللنا المقدار المعطى إلى عاملين .

والمثال التالي يوضح ذلك .

 مثال :

حلل المقدار س² _ 4 إلى عاملين إن أمكن باستخدام البطاقة والقطع الجبرية ؟

        الحل :

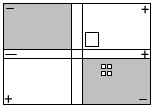
                أما الخطوة الثالثة فيوضحها الشكل التالي :

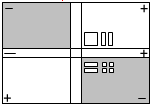
            أما الخطوة الرابعة فيوضحها الشكل التالي :   

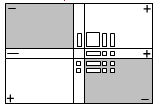
أي أن س² _ 4 = ( س + 2 ) ( س _ 2 ) .          وهو المطلوب .

       نشاط :

                حلل المقدار س² _ 9 إن أمكن باستخدام البطاقة والقطع الجبرية .

       الحل :

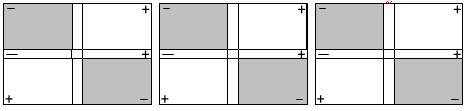
مثال :

                حلل المقدار 4 س² _ 9 إن أمكن باستخدام البطاقة والقطع الجبرية ؟

        الحل :

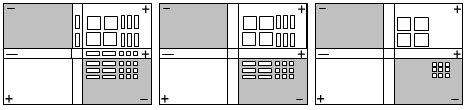
أي أن 4 س² _ 9 = ( 2 س + 3 ) 2 س _ 3 )  وهو المطلوب .

وبعد هذا العرض بطريقة محسوسة يمكن للمعلم أن يعطي أمثلة لمقادير تحلل بطريقة مجردة والأمثلة التالية توضح ذلك .

مثال :

                حلل المقادير التالية بطريقة تمييز المتطابقة .

                          أ ) س² + 14 س + 49 .

                        ب ) س² _ 14 س + 49 .

                         ج ) س² _ 49 .

        الحل :

                  أ ) س² + 14 س + 49 = ( س + 7 )²

                ب ) س² _ 14 س + 49 = ( س _ 7 )²

                ج ) س² _ 49 = ( س + 7 ) ( س _ 7 )

التقويم :

1-             ميز العبارة التي تمثل مربعاً كاملاً فيما يلي :

  أ  ) س² + 10 س + 25

ب ) 2 س² _ 16 س _ 32

2-             حلل ما يلي بطريقة تمييز المتطابقة :

أ  ) 4 س² + 2 س + 1

ب ) 9 س² _ 27

الواجب المنزلي :

        حلل ما يلي بطريقة تمييز المتطابقة :

 أ  ) 4 س² _ 4 س + 1

ب ) 4 س² _ 25