

النسبة :
عندما نستعمل كسر ما من أجل المقارنة بين عددين أو مجموعتين ، فإننا نسمي هذا الكسر نسبة فمثلا:
إذا كان لدينا مجموعتين على النحو التالي ، فما هو الكسر الذي يمثل نسبة عدد المجموعة الأولى إل عدد المجموعة الثانية ؟
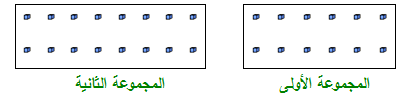
إذن نسبة عدد المجموعة الأولى إلى عدد المجموعة الثانية
=
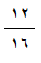
وتكتب النسبة على الصورة التالية 12 : 16
وتقرأ 12 إلى 16 .
أمثلة : أكتب النسبة حسب السهم المشار ؟

الجواب :
( 8 : 6 ) =
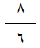
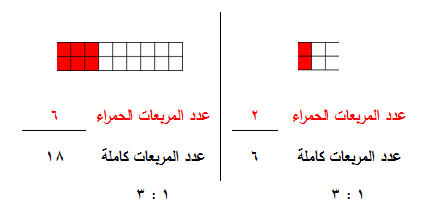
مثال : أكتب النسب التالية في أبسط صورة ؟
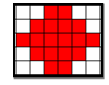
أ ) نسبة الأجزاء الحمراء إلى الأجزاء
البيضاء ؟ ( 3 : 2 )
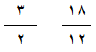
ب ) نسبة الأجزاء البيضاء إلى الأجزاء الحمراء ؟ ( 2 : 3 )
ج ) نسبة الأجزاء الحمراء إلى جميع الأجزاء ؟ 18 :30 = 3 : 5
د ) نسبة الأجزاء البيضاء إلى جميع الأجزاء ؟ 12 : 30 = 2 : 5
· نسبة مقدارين :
س : طريقان طول الأول 2000 م وطول الثاني 3 كم ، ما نسبة طول الطريق الأول إلى طول الطريق الثاني ؟
ج : للإجابة على السؤال لابد من تحويل أحد الوحدات إلى الأخرى كالتالي :
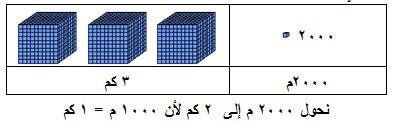
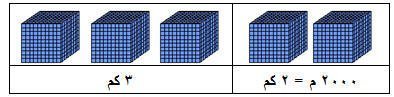
وتصبح النسبة كالتالي : 2 : 3 وبالمثل لو حولناها بالمتر فالنسبة ثابتة
· التناسب :
نسبة المربعات الحمراء إلى كل الشكل :

ومن هذه الخاصية تنتج خاصية أخرى وهي


· النسبة المئوية :
غالبا ما يتم تدريس التطبيقات على درس النسبة المئوية بحل مسائل تحتاج لفهم التناسب وأحيانا تحتاج إلى الجبر وهذا الأسلوب غالبا ما يكون صعبا لعدم إتقانهم المفاهيم الجبرية ، وهناك أسلوب أقل صعوبة لتدريس مفهوم النسبة المئوية على أنها جزء من مائة
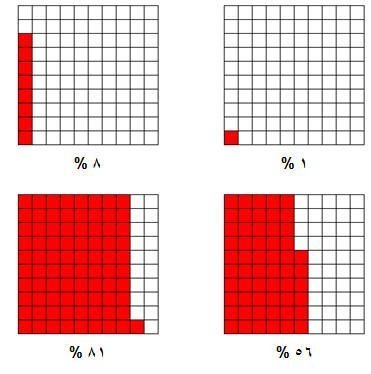
ويمكننا استخدام المربع 10 × 10 في حل العديد من المسائل على النسبة المئوية ولكن يفضل قبل حل المسائل أن يتعامل الطلبة مع صورة للمربع المضلل وتظليل جزء منه أو إعطائهم جزء مضلل ويطلب منهم تحديد نسبة الجزء المضلل :
وكذلك نستطيع تمثيل أكثر من واحد في المائة وأقل من واحد في المائة كالمثال التالي :
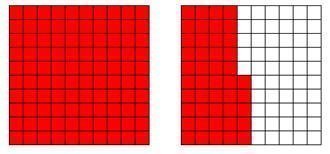
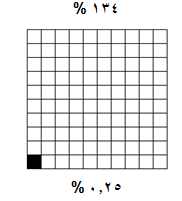

وبالتالي إذا كان المربع الكبير يمثل عددا معينا فإن المربع الصغير يمثل هذا العدد مقسوما على 100 مثلاً .
مثال : إذا كان المربع الكبير يمثل 800 شخص فأوجد الآتي :
أ ) عدد الأشخاص الذين يمثلهم ربع المربع الصغير ؟
ب ) عدد الأشخاص الذين يمثلهم نصف المربع الصغير ؟
ج ) الجزء الذي يمثل 400 شخص .
د ) الجزء الذي يمثل 200 شخص .
هـ ) الجزء الذي يمثل 80 شخص .
و ) الجزء الذي يمثل 8 أشخاص .

الجواب : مجموع الأشخاص 800
أ ) ربع المربع يمثل شخصان .
ب ) نصف المربع يمثل 4 أشخاص
ج ) 400 شخص يمثلون 50% .
د ) 200 شخص يمثلون 25 % .
هـ ) 80 شخص يمثلون 10%
و ) 8 أشخاص يمثل 1 % .
مثال : لدى تاجر بضاعة ورفع سعرها 60% فأصبح السعر الجديد 384 ريالاً ، فكم كان سعر البضاعة قبل البيع ؟

الجواب : سعر البضاعة الأصلي يمثل 100% ثم زاد التاجر البضاعة بنسبة 60 % ليصبح السعر 160% ومقداره 384 ريالاً
إذن المربع الصغير الواحد يمثل 384 ÷ 160 = 2.4 ريالاً
وعليه فإن المربع الكبير 100 % = 2.4 ×100 = 240 ريالاً
مثال : تبرع رجل محسن بخمسة وعشرين فدان واشترط أن تكون منها 6 فددين حدائق عامة ، فما هي النسبة المئوية للحدائق العامة؟
الجواب :
أولاً نمثل الخمسة والعشرين فدانا على المربع الكبير وبالتالي تكون قيمة المربع الصغير 25 ÷ 100 = 0.25 أي أن المربع البصغير يمثل ربع فدان وبالتالي فإن 4 مربعات صغيرة تمثل فدان واحد إذن 6 فدادين = 24 مربع أي 24% من عدد الفدادين الكامل .
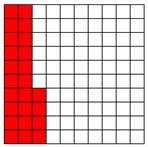
ونستعرض الآن بعض الأمثلة التي يمثل فيها النسبة أكبر من 100 ، وإليك بعض هذه الأمثلة :
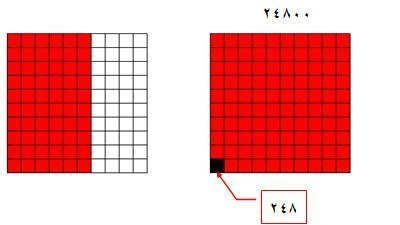
مثال : إذا كانت أرباح أحد المحلات في هذه السنة 24800 ريال فإذا زادت الأرباح بنسبة 60% في السنة التالية فكم أرباح المحل في السنة التالية ؟
الجواب :
يمكن تمثيل الأرباح بالمربع الكبير ، وعليه فإن 100 مربع تمثل الأرباح الحالية أي 24800 ريال وبالتالي فإن المربع الصغير يمثل 24800÷100=248 أما الأرباح التي تمثل 60 مربعا في السنة التالية هي 60 × 248 = 14880 ريالا .
وعليه فإن اجمالي الأرباح هي :
24800 + 14880 = 39680 ريالاً .
والرسم التالي يوضح الفكرة :
مثال : إذا أعلنت أحد المكتبات عن تخفيض قدره 20 % على سعر مجموعة من الكتب فإذا دفع الرجل مبلغ 88 ريالا ثمنا لهذه الكتب بعد التخفيض ، فكم كان سعره قبل التخفيض ؟
الجواب : في هذا النوع من التمارين تحدد قيمة السلعة بعد التخفيض والمطلوب معرفة السعر بعد التخفيض .
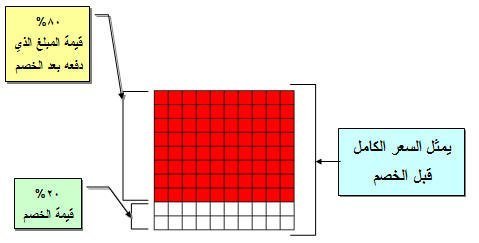
فيصبح ما دفعه الرجل يمثل 80% من القيمة الأصلية للقلم ، وبالتالي فإن :
80 مربعا صغيرا يمثل 88 ريال
والمربع الصغير يمثل 88 ÷ 80 = 1.1
والمربع الكبير يمثل 1.1 × 100 = 110 ريالاً
مثال : اشترى رجل أرضا بمبلغ معين ثم باعها بمبلغ 850000 ريالاً فإذا ربح 240% من سعر الأرض ، فبكم اشتراها ؟
الجواب : يعتبر هذا النوع من التطبيقات من أصعب الأنواع ، وبالرغم من ذلك يمكن حلها بنفس الطريقة على النحو التالي :
وبالتالي فإن : 340 مربعا تمثل سعر البيع أي أن كل مربع يساوي
لأن الربح يمثل 240% والسعر الأصلي 100% = 340%
850000 ÷ 340 = 2500 ريالاً ،
وعليه فإن السعر الأصلي = 2500 × 100 = 250000 ريالاً .
وللتأكد : ( 250000 × 240 ) ÷ 100 = 600000
سعر البيع = سعر الشراء + سعر البيع
= 250000 + 600000 = 850000 ريالاً .