النمذجة باستخدام الشرائح
في الرياضيات
الرياضيات السنغافورية هي منهج لتدريس الرياضيات وجد في سنغافورة عام 1982م
وانتشر هذا المنهج خارج سنغافورة منذ العام 1998م بعد أن أثبت الطلاب السنغافوريين
مستواهم المتقدم في الرياضيات
( النمذجة في الرياضيات ) :
هي وسيلة غير تقليدية للتعبير عن معطيات مسائل الرياضيات و طرق الوصول للحل بكل يسر و إيضاح. يستخدم فيها الرسم ( الصورة ) بالأشكال و الألوان المختلفة و الإرشادات الكتابية علي الرسم للتعبير عن العلاقات و العمليات و الاستنتاجات الحسابية للمسائل
وتعد النمذجة باستخدام الشرائح أحد الاستراتيجيات الأساسية التي يقوم عليها منهج الرياضيات السنغافوري.
وفيما يلي سنركز على هذه الاستراتيجية باستعراض بعض المسائل اللفظية المتوافقة مع المنهج السنغافوري وطريقة حلها باستخدام هذه الاستراتيجية بالاستفادة من برمجية نمذجة المسائل اللفظية
برمجية نمذجة المسائل
الرياضية اللفظية Thinking Blocks :
يعتبر حل المسألة
الرياضية اللفظية من أصعب المسائل الرياضية التي يجد الطلاب صعوبةً بالغةً في
التعامل معها
.
تعد برمجية Thinking Blocks من أفضل البرمجيات التعليمية التي تساعد الطلاب في التغلب على هذه الصعوبة.
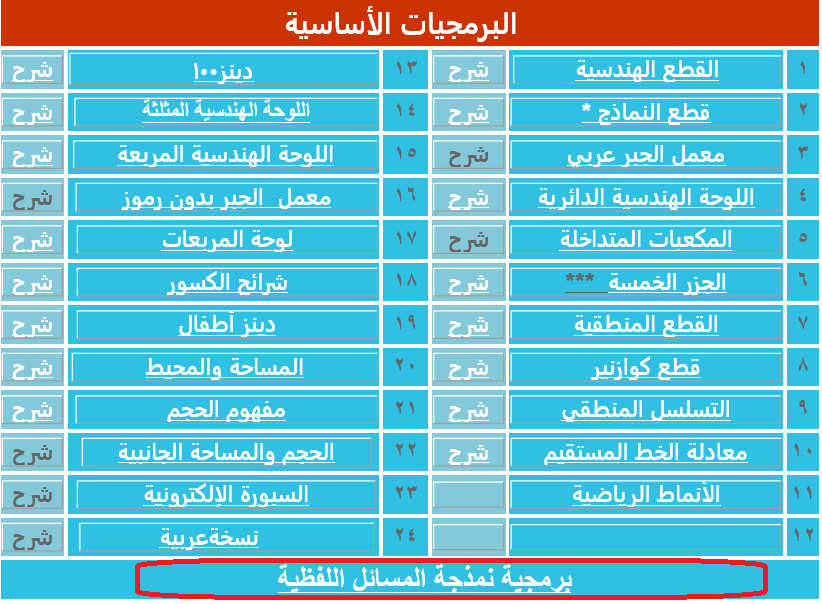
ويمكن الوصول إلى هذه البرمجية من موقع التعليم الالكتروني لتطوير تدريس الرياضيات (www.aghandoura.com) من البرمجيات الأساسية.


وعند
الدخول إلى البرمجية من خلال  تظهر صفحة العمل في البرمجية :
تظهر صفحة العمل في البرمجية :

مثال:
استخدام برمجية Thinking Blocks في حل المسألة التالية:
اشترى أحمد كتاب
قيمته 5 ريالات . وبقي معه 19 ريال . كم كان معه من البداية ؟
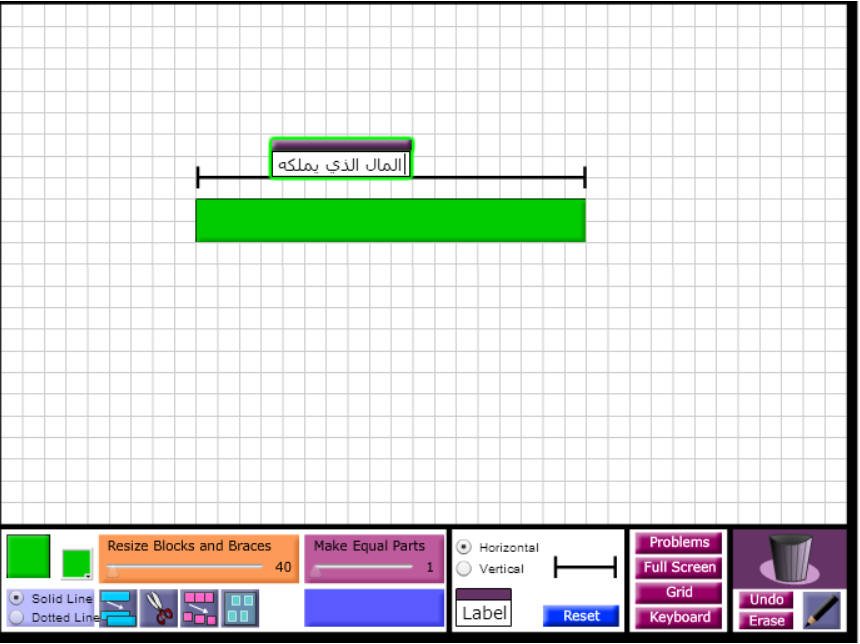
المال الذي يملكه احمد والذي
لانعرف كم هو وعلينا استنتاجه
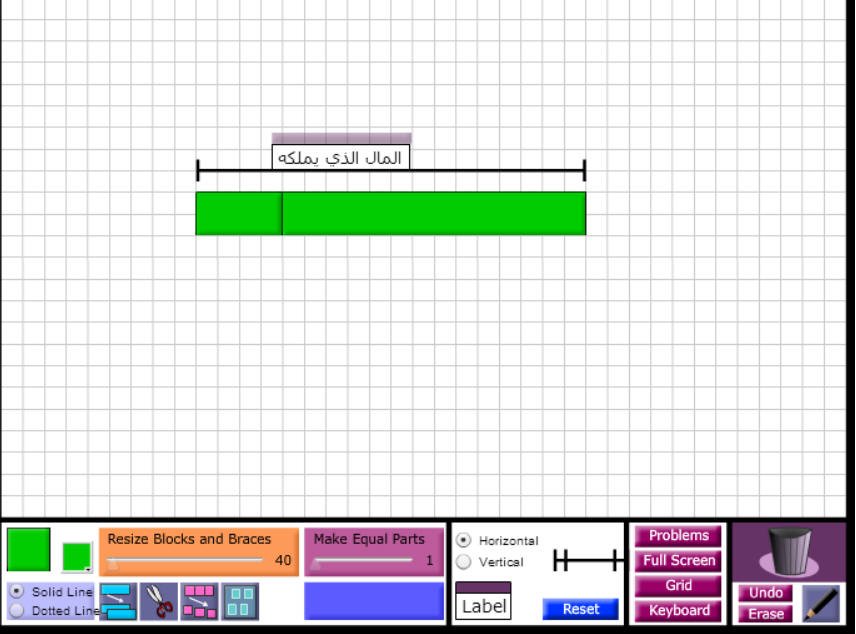
نجزء
القطعة لمعرفة المال الذي يملكه
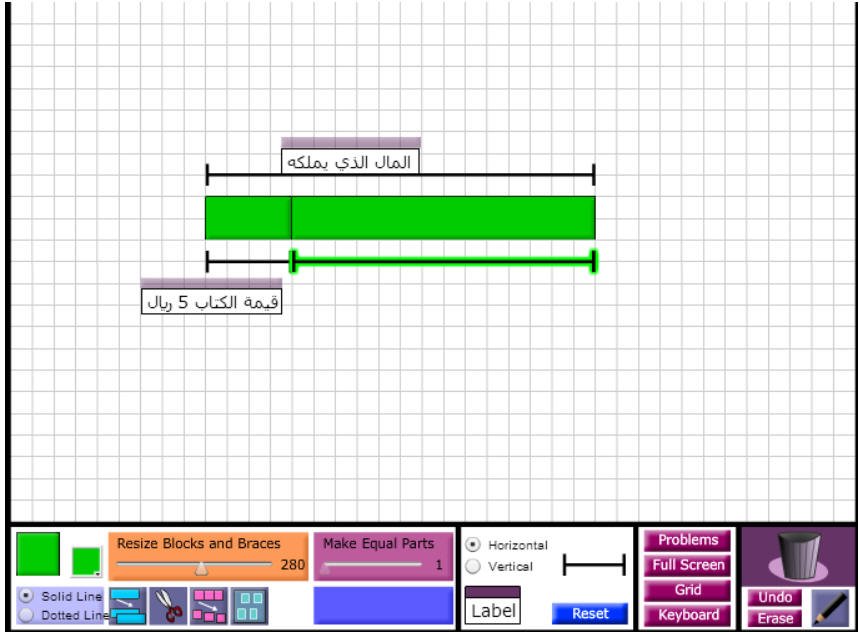
نضع قيمة الكتاب العلومة في السؤال وهي 5 ريال وتمثل الجزء الصغير من المبلغ الذي يملكه
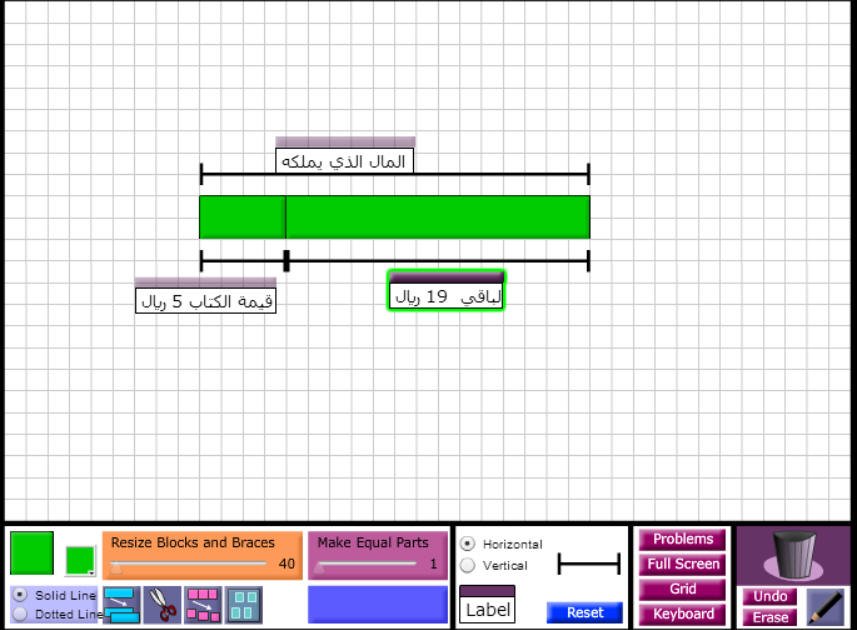
المبلغ الذي اشترى به الكتاب 5 ريال والمتبقي معه 19 . تبقى أن نقوم بالعملية
الحسابية لمعرفة المال الذي يملكه :
قيمة الكتاب + الباقي من المبلغ = مجموع ما يملكه احمد
19+5 = 24 ريال وهو ما يملكه احمد
وسوف نستخدم هذه البرمجية في حل بعض مسائل الرياضيات السنغافورية لتحقيق النمذجة
مسائل
التدريب على حل أنواع الأسئلة الموجودة في البرمجية
حل الأسئلة المتنوعة حسب درجاتها ونوعها
بالضغط علي أيقونة problems تظهر شاشة جديدة:
الأيقونة الزرقاء : فتح نافذة كتابة المسائل من المستخدم .
الأيقونة الخضراء: للدخول إلى المسائل المنمذجة.
( 1 ) مسائل الجمع و الطرح
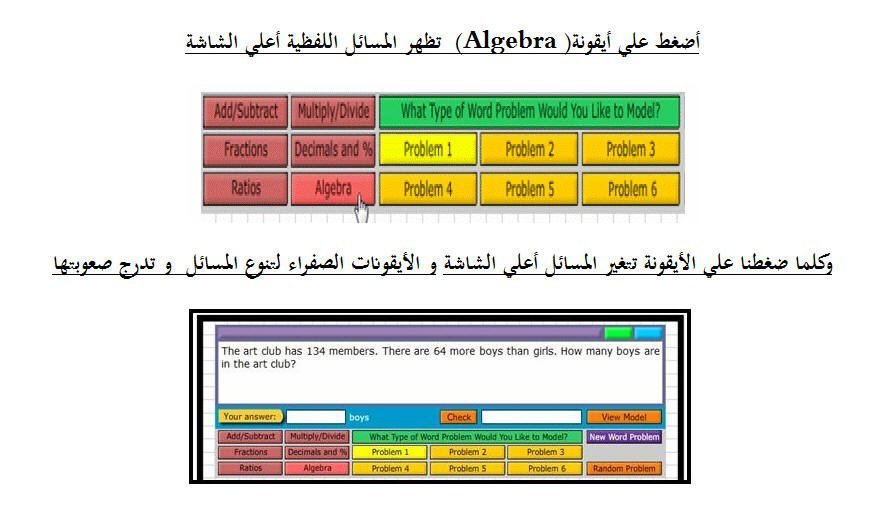
أضغط علي أيقونة ( Add / Subtract )تظهر المسائل اللفظية أعلي الشاشة

وكلما ضغطنا علي الأيقونة تتغير المسائل أعلي الشاشة و الأيقونات الصفراء لتنوع المسائل و تدرج صعوبتها

مثال علي الجمع و الطرح
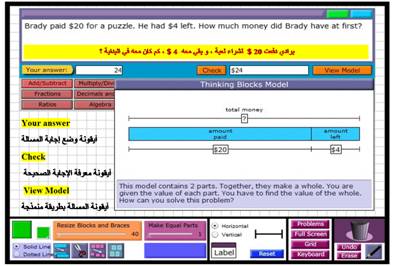
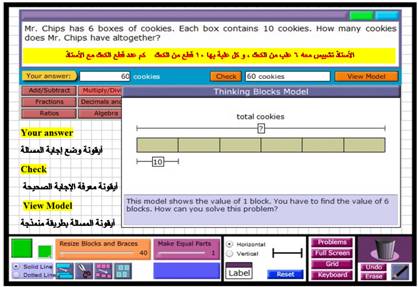
( 2 ) الضرب و القسمة
أضغط علي أيقونة ( Multiply / Divide )تظهر المسائل اللفظية أعلي الشاشة
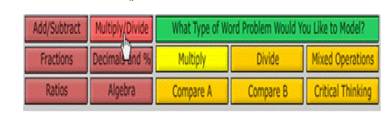
وكلما ضغطنا علي الأيقونة تتغير المسائل أعلي الشاشة والأيقونات الصفراء لتنوع المسائل و تدرج صعوبتها
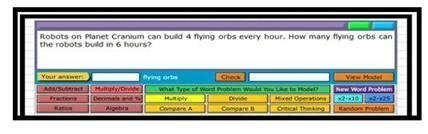
مثال علي الضرب و القسمة
( 3 ) مسائل علي الكسور
أضغط علي أيقونة ( Fractions )تظهر المسائل اللفظية أعلي الشاشة
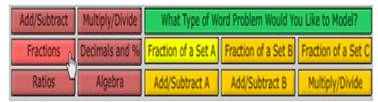
وكلما ضغطنا علي الأيقونة تتغير المسائل أعلي الشاشة والأيقونات الصفراء لتنوع المسائل و تدرج صعوبتها
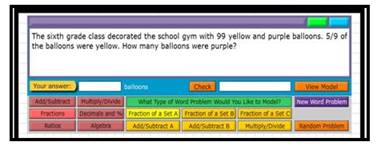
مثال علي الكسور
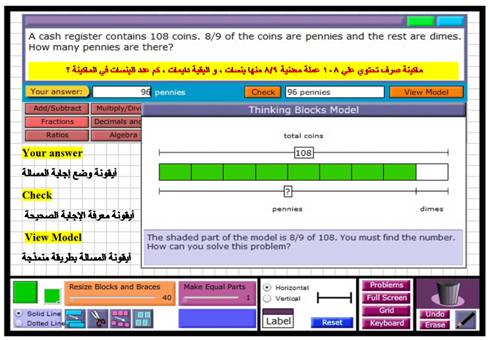
( 4 ) مسائل علي الأعداد العشرية و النسب المئوية
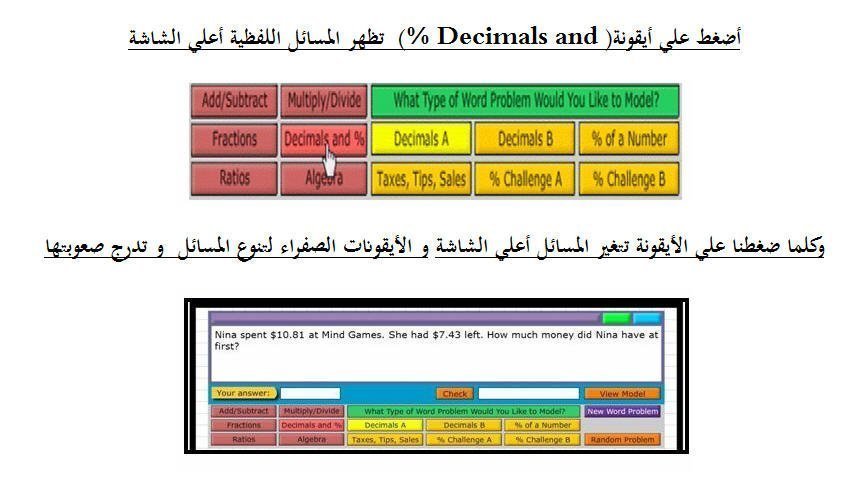
مثال علي الأعداد العشرية و النسب المئوية
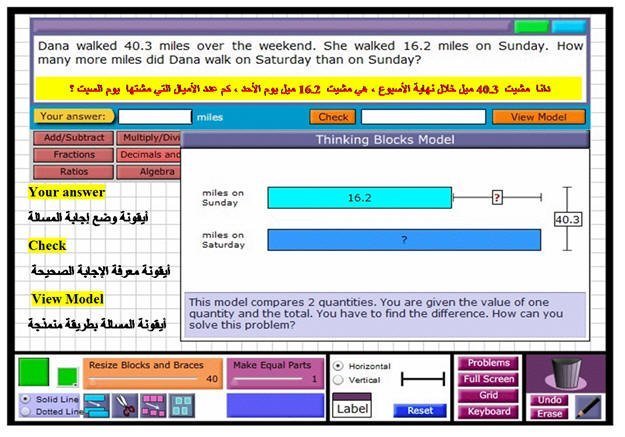
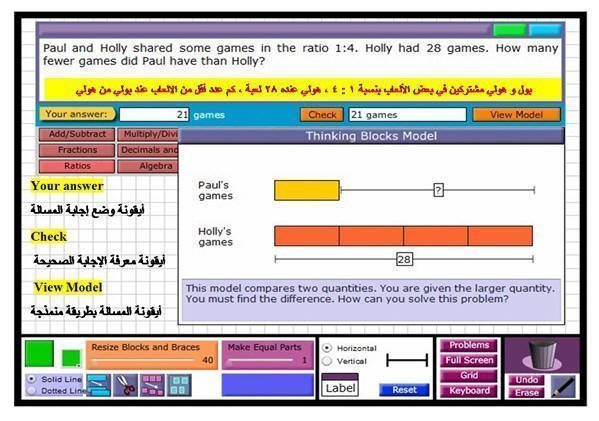
( 5 ) مسائل علي النسبة
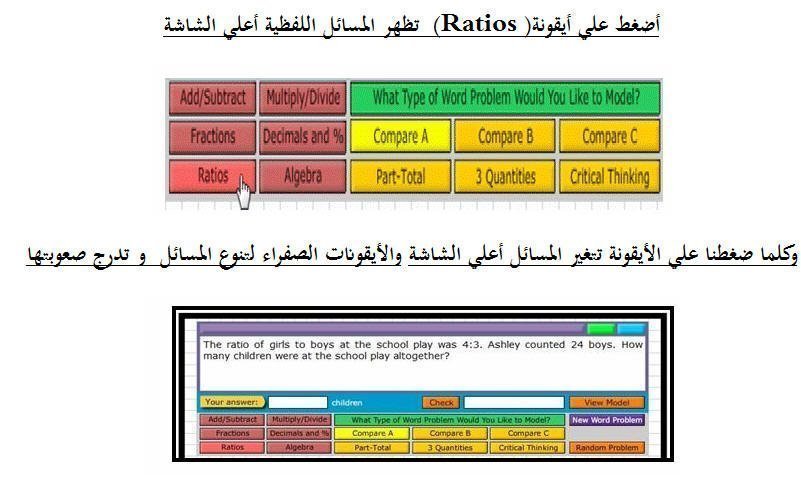
مثال علي النسبة
( 6 ) مسائل علي الجبر
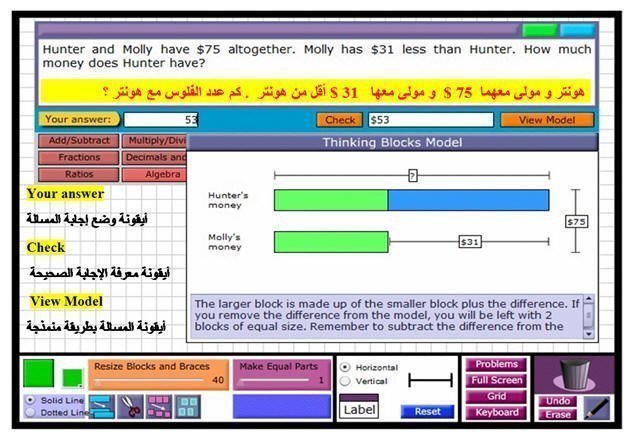
مثال علي الجبر
ملاحظات هامة:
( 1 ) أيقونة جلب مسائل جديد من نفس النوع الذي تم اختياره
نضغط بالمؤشر على أيقونة مسألة جديد
 تظهر
لنا مسألة جديدة .
تظهر
لنا مسألة جديدة .
( 2 ) أيقونة جلب مسائل عشوائية
نضغط على أيقونة المسائل العشوائية
 نشاهد
مسألة جديدة .
نشاهد
مسألة جديدة .
فيما يلي عدد من المسائل اللفظية على غرار المسائل السنغافورية :
مسألة (1)
( 1 ) عمرو و زيد يملكان 520 ريال ، إذا صرف عمرو 2/5 ما يملكه ،و صرف زيد 40 ريال ، تبقي لديهما نفس القدر من المال . كم يملك كلا منهما ؟
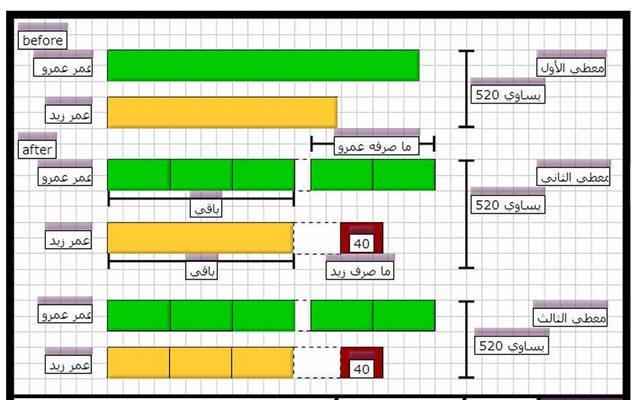
بحذف العدد ( 40 ) من الطرفين
لاحظ ( 8 ) مربعات متساوية قيمتهم 480) ) ريال
قيمة المربع الواحد = قيمة المربعات ( 480 ) ÷ عدد المربعات ( 8 ) = 60 ريال
ما يملكه عمرو = عدد مربعاته ( 5 ) × قيمة المربع ( 60 ) = 300 ريال
ما يملكه زيد = عدد مربعاته ( 3 ) × قيمة المربع ( 60 ) + 40 ريال = 180 + 40 = 220 ريال
الحل الجبري

مسألة (2) :
عمرو يبلغ عمره ربع عمر زيد ، بعد خمس سنوات أصبح عمر عمرو ثلث عمر زيد . فكم أعمارهم ؟
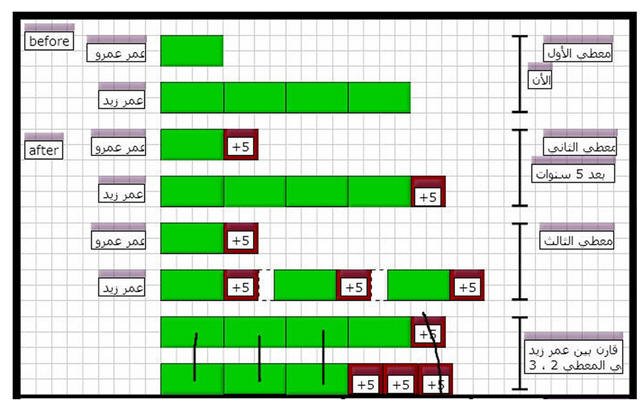
بعمل مقارنة بين عمر زيد في المعطيين ( الثاني و الثالث )
نلاحظ ان قيمة المربع الواحد = 10 سنوات
عمر عمرو الآن = عدد مربعاته ( 1 ) × قيمة المربع ( 10 ) = 10 سنوات
عمر زيد الآن = عدد مربعاته ( 4 ) × قيمة المربع ( 10 ) = 40 سنه

مسألة (3) :
حضانة أطفال تحوي 40 طفلا ،30 % منهم ذكور ، عندما عاد بعض الذكور إلي بيوتهم انخفضت نسبة الذكور إلي20 % ، كم يبقي من الذكور في الحضانة ؟
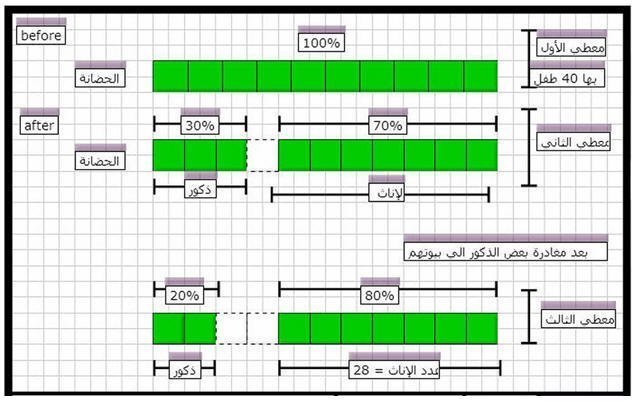
لاحظ في المعطي الأول
( 10 ) مربعات متساوية قيمتهم 40) ) طفل
قيمة المربع الواحد = قيمة المربعات ( 40 ) ÷ عدد المربعات ( 10 ) = 4 طفل
لاحظ في المعطي الثاني
عدد الإناث = عدد مربعاتها ( 7 ) × قيمة المربع ( 4 ) = 28 طفل
عدد الذكور = عدد مربعاته ( 3 ) × قيمة المربع ( 4 ) = 12 طفل
لاحظ في المعطي الثالث
بعد مغادرة بعض الذكور ( الحضانة( إلي بيوتهم
عدد الذكور تغير عددياً ( ؟ ) و أصبحت نسبته تمثل 20 % عدد مربعاته ( 2 )
عدد الإناث لم يتغير عددياً ( 28 ) و أصبحت نسبتها تمثل 80 % عدد مربعاتها ( 8 )
قيمة المربع الواحد = قيمة المربعات ( 28 ) ÷ عدد المربعات ( 8 ) = 3.5 طفل
عدد الذكور الباقية = عدد مربعاته ( 2 ) × قيمة المربع ( 3.5 ) = 7 طفل
الحل الجبري

مسألة (4) :
( 4 ) استلمت نوره الراتب في أول الشهر و قد صرفت ربعه في الأسبوع الأول من الشهر ، ثم صرفت ثلثي الباقي في الأسبوع الثاني . فما نسبة المتبقي لها من الراتب حتى أخر الشهر ؟
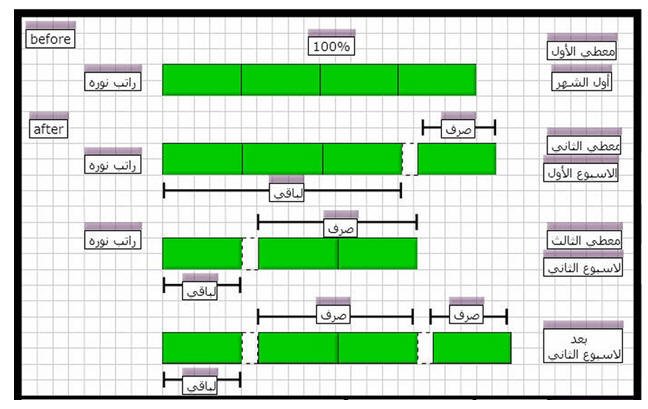
لاحظ بعد الأسبوع الثاني
عدد مربعات الراتب كاملاً = 4
عدد مربعات المصروف من الراتب = 3
عدد مربعات الباقي من الراتب = 1
نسبة المتبقي من الراتب = عدد مربعات الباقي من الراتب ( 1 ) ÷ عدد مربعات الراتب كاملاً ( 4 )= 1/4
الحل الجبري

مسألة (5):
أرض زراعية ثلث منها مزروع ذرة ، و ربع منها مزروع شوفانا ، و الباقي 20 فدان مزروعة أرز . فكم فدانا تبلغ المساحة ؟
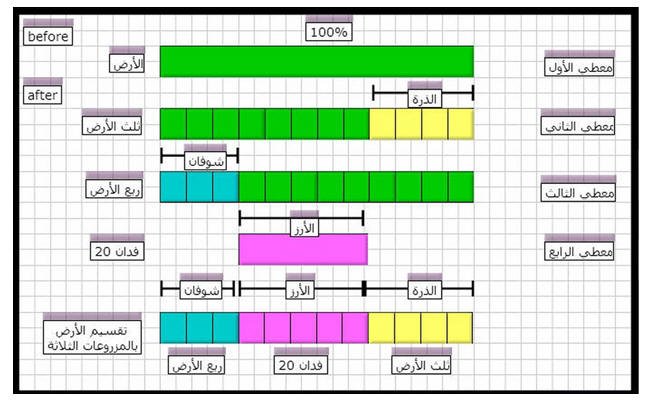
تم تقسيم الأرض إلي 12 مربعاً ( لسهول تقسيم بين الثلث و الربع )
عدد مربعات الذرة ( 4 )
عدد مربعات الشوفان ( 3 )
عدد مربعات الأرز ( 5 ) و قيمتها ( 20 ) فدان
قيمة المربع الواحد = قيمة المربعات ( 20 ) ÷ عدد المربعات ( 5 ) = 4 فدان
مساحة الذرة = عدد مربعاته ( 4 ) × قيمة المربع ( 4 ) = 16 فدان
مساحة الشوفان = عدد مربعاته ( 3 ) × قيمة المربع ( 4 ) = 12 فدان
مساحة الأرض = مساحة الذرة ( 16 )+ مساحة الشوفان ( 12 )+ مساحة الأرز( 20 ) =48 فدان
الحل الجبري
