النسبة المئوية :
تعتبر دروس النسبة المئوية من الدروس التي يواجه فيها كثير من التلاميذ بعض الصعوبة وتبرز أهمية هذه الدروس في أن التلاميذ دائماً ما يقابلون مسائل النسبة المئوية حتى في حياتهم اليومية ، ولذلك يجب أن نحاول قدر الإمكان توصيل هذه الدروس بأفضل وأسهل الطرق التي تكفل للتلاميذ فهماً أفضل وبقاءً أكثر ، ومن أفضل طرق عرض دروس النسبة المئوية اللوحة الهندسية التي تساعد كثيراً على استيعاب هذه الدروس ، وسنحاول الآن عرض هذه الطريقة باستخدام اللوحة الهندسية:
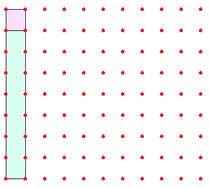
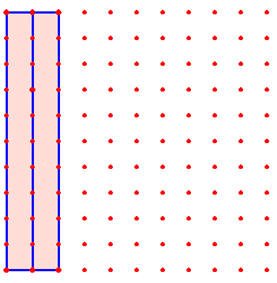
في الشكل المجاور صورة للوحة هندسية وتحتوي على مئة مربع . ستكون اللوحة عبارة عن النسبة كاملة 100% ،إذن الشريط الواحد وهو عبارة عن عمود يمثل 10% ، والمربع الواحد يمثل 1% .

امثلة :
مثل على اللوحة 35%
مثال 2
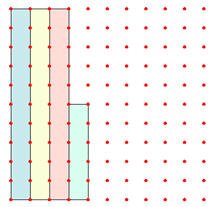
حدد النسبة الموضحة على اللوحة والتي تظهر في الشكل التالي :
الحل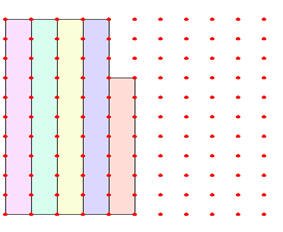
إن التلاميذ سيقومون بتحديد عدد المربعات المحددة على اللوحة ، وبالتأكيد ستكون الإجابة أن النسبة هي 47 %
مثال 3 :
حدد النسب في كل مما يلي :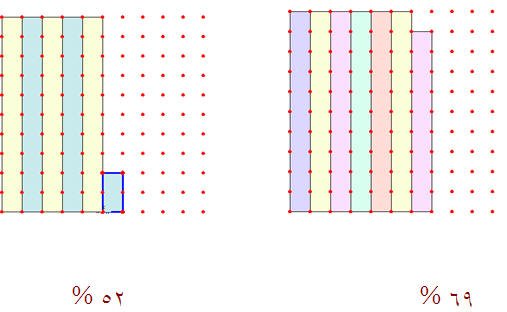
مسائل على النسبة المئوية :-
مثال 1
اذا كان عدد الناجحين في إحدى المواد الدراسية 700طالب وكانت نسبة النجاح هي 20 % فكم هو عدد الطلاب الكلي ؟
الحل :
تتلخص فكرة الحل في أن التلميذ يحدد ما يمثله المربع الصغير ،لذلك فإن 20% أي 20 مربعاً صغيراً تمثل عدد الناجحين أي :
700 ÷ 20 = 35 أي أن المربع الواحد يمثل 35 ، وعدد الطلاب الكلي هو عدد مربعات اللوحـة إذن 35 ×100 =3500 وهو عدد الطلاب الكلي وعلى اللوحة تظهر نسبة الطلاب الناجحين إلى عدد الطلاب الكـلي .
مثال 2:-
إذا كان لدى تاجر بضاعة ورفع سعرها 60 % فأصبح السعر الجديد 384 ريالاً ، فكم كان سعرها قبل رفعه السعر ؟
الحل :
إن سعر البضاعة قبل رفع السعر يمثل بالمربع الكبير أما الزيادة 60 % فهي تمثل بـ60 مربعاً إضافة على المربع الكبير ، كما يظهر على الشكل التالي من خلال اللوحة :
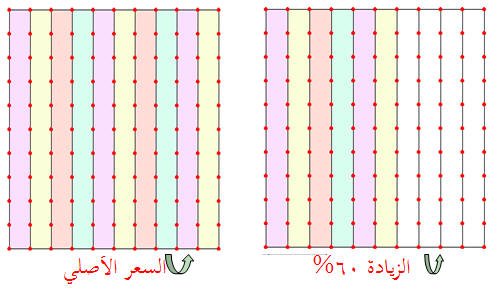
الآن السعر الجديد هو ما يمثله السعر الأصلي إضافة إلى الزيادة أي أن الشكلين معاً يمثلان السعر الجديد وبالتالي :
384 ÷ 160 = 2,4 وهي قيمة المربع الصغير ,السعر الأصلي قبل أن يرفعه التاجر = 2,4 × 100 = 240 ريالاً
مثال 3 :-
كان عدد التلاميذ في أحد الصفوف الدراسية في السنة الماضية 25 تلميذاً ثم ازداد هذه السنة بنسبة 20% فكم أصبح عدد التلاميذ ؟
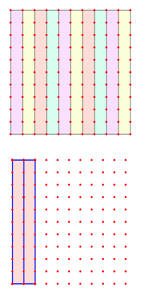
الحل :
إن المربع الكبير يمثل عدد التلاميذ في السنة الماضية إذن المربع الواحد 25÷100 =0,25مقدار الزيادة هو 20% أي تمثل 20 مربعاً ,مقدار الزيادة = 025×20= 5 طالب ,عدد الطلاب =20+5 =25 هذه السنة ,والشكل الأول يوضح نسبة الطلاب السنة الماضية ,والشكل الثاني يوضح نسبة الزيادة هذه السنة
مثال 4 :-
لفة قماش طولها 40متراً ، قص تاجر الأقمشة 15 % من اللفة فكم هو طول الجزء المقصوص ؟
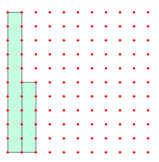
لفة القماش كاملة(40 م ) تمثل المربع الكبير إذن المربع الواحد 40 ÷ 100 = 0,4 , إذن الجزء المقصوص= 0,4 × 15= 6 أمتار
مسائل على الربح والخسارة:-
تربح شركة سنوياً 400000ريال فإذا كانت توزع أرباحها كما يلي:
30% رواتب موظفين ، 15% صيانة ، 10% مكافآت ، والباقي يوزع على المساهمين ، فأوجد حصة كل مجال منها ؟

الحل :
المربع الكبير المجاور يمثل الأرباح السنوية أي :
أنه يمثل 400000 وبالتالي :
المربع الصغير = 400000÷ 100=4000
وعليه : حصة رواتب الموظفين = 30× 4000=120000ريال
نصيب الصيانة من الأرباح = 15× 4000 = 60000ريال
نصيب المكافآت من الأرباح = 10× 4000 = 40000ريال
والباقي يوزع على المساهمين بعد جمع المبالغ السابقة فيصبح نصيب المساهمين =400000 -220000 =180000ريالمثال 2 :-
إذا كان ربح أحد المحلات التجارية في هذه السنة 21500ريال فإذا زادت الأرباح هذه السنة بمقدار62% فكم أرباح المحل في السنة التالية:
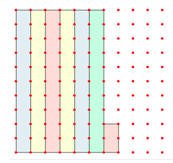
الحل :
المربع الواحد=21500÷100=215
الأرباح في السنة التالية 62×215=13330
مجموع الأرباح=13330+21500=34830مسائل على التخفيضات :-
مثال:
إذا كان ثمن أحد أجهزة التسجيل 120 ريالاً فإذا خصم البائع 5 % من ثمن الجهاز عند الدفع فوراً ، فما ثمن الجهاز بعد التخفيض ؟
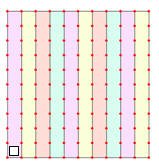
الحل
ثمن الجهاز 120 تمثل بالمربع الكبير، وبالتالي المربع الواحد الصغير = 120 ÷100=1,2 , قيمة التخفيض = 5× 1,2 =6 ريال
ثمن الجهاز بعد التخفيض =120 – 6 = 114ريالمسائل متقدمة :-
عرضت إحدى المحلات التجارية الإعلان الدعائي التالي :
عند شرائك بقيمة 150ريال تحصل على تخفيض قدره 10% وإذا تم الدفع فوراً تحصل على تخفيض قدره 5 % فكم يصبح إجمالي التخفيض
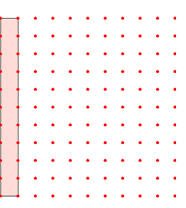
الحل :هذه المسألة تتكون من شقين :أي أن هناك تخفيضان :
أولاً :
القيمة قبل التخفيض وهي 150 تمثل المربع الكبير ، إذن المربع الصغير =150÷100=1,5 قيمة التخفيض الأول = 1,5 × 10 = 15 ريال
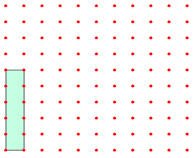
القيمة بعد التخفيض الأول = 150 –15 = 135 ريال .
ثانياً :
الآن 135 ريالاً هي التي تمثل المربع الكبير المربع الصغير = 135 ÷ 100= 1,35
إذن :
مقدار التخفيض الثاني =1,35×5=6,75 ,قيمة الشراء بعد التخفيض الثاني = 135 – 6,75 =128,25ريال
مثال 2 :-
اشترى رجل منزلاً ثم باعه بمبلغ وقدره 650000ريال فإذا ربح 225% من سعر المنزل ، فبكم اشترى المنزل ؟
الحل :
225% هي زيادة على سعر المنزل الأصلي أي أن المربع الكبير يمثل سعر الشراء أي 100% والزيادة تمثل 225 % ويظهر ذلك كما يلي:
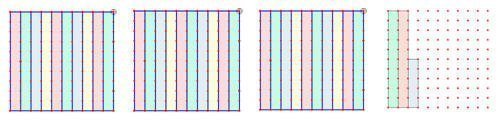
المربع الصغير = 650000÷100= 2000
السعر الأصلي = 2000 × 100 = 200000ريال