الوحدة الثالثة الأعداد المتتالية:

نشاط :

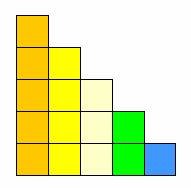
خذ عدداً من المربعات أو المكعبات المتداخلة لبناء أعداد متتالية 1 ، 2 ، 3 ، 4 ، 5

قم ببناء شكل آخر مماثل له بدوران 180 درجة علي النحو التالي

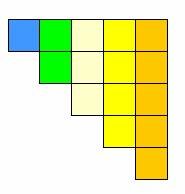
ضم الشكلين معاً لتكوين مستطيل  كما في الشكل التالي :

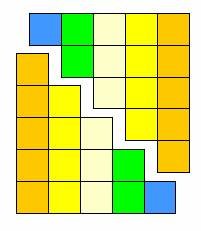
كم طول هذا المستطيل ؟ كم عرضه ؟

ما العلاقة بين عدد الأعداد المتتالية وطول المستطيل ؟

كرر النشاط السابق وقم ببناء مستطيلات من أعداد متتالية مختلفة بدءاً من الواحد وأكمل الجدول التالي :

الخلاصة :

   ·   الصيغة العامة للأعداد الزوجية هي 2ن

   ·   الصيغة العامة للأعداد الفردية هي (2ن-1)

   ·   زوجي + زوجي            زوجي

   ·   فردي + فردي              زوجي

   ·   فردي + زوجي              فردي

   ·   مجموع عدد معين من الأعداد الفردية المتتالية المبدوءة بالحد الأول يساوي ن تربيع

(مربع عدد الحدود) حيث ن تساوي عدد الأعداد الفردية المطلوب جمعها .

   ·   مجموع عدد معين من الأعداد الزوجية المتتالية المبدوءة بالحد الأول يساوي ن(ن+1)

        حيث ن عدد الحدود المطلوب جمعها .

   ·   مجموع عدد معين من الأعداد المتتالية المبدوءة بالواحد يساوي

                    ن(ن+1)

                         2    

حيث ن تمثل عدد الأعداد المطلوب جمعها .

أما إذا أردنا جمع سلسلة من الأعداد غير المبدوءة من الواحد  مثل :

12 ، 14 ، 16 ، 18 ، 20 فهناك طريقة أخرى تعتمد على الطرح وتتلخص في إيجاد مجمــوع سلـسـلة الأعــداد التي حـدها الأخـير هو 20 ، أي أن عـدد الحدود هو عشـرة (وذلك بقسمة 20 على 2 لمعرفة عدد الحدود) ثم طرح مجموع السلسلة المكونة من الحدود التي تسبق الحد الأول (12) ( أي الخمسة حدود الأولى ) نظراً لأن ذلك الحد هو عشرة .

                ن(ن+1)  - م(م+1)  حيث م عدد حدود الجزء الأول من المتسلسلة

                10 × 11 - 5 × 6  =

                    110  -  30     = 80

وهناك طريقة مختصرة لإيجاد المجموع إذا عُرف الحد الأول والحد الأخير تتلخص في أن :

                المجموع = (الحد الأول + الحد الأخير) × عدد الحدود

                                                                2 

                =   (12 + 20) × 

                =    = 80

وفي حالة عدم معرفتنا للحد الأخير كأن يطلب منك إيجاد مجموع العشرة حدود في المتتالية 4 ، 6 ، 8 ، + 10 ، .............  يتوجب علينا معرفة الحد الأخير وفق القاعدة التالية :

        الحد الأخير = الأول + ( عدد الحدود - 1) × مقدار الزيادة

فعلى سبيل المثال : 12 + 14 + ......  خمسة حدود ومقدار الزيادة 2

        الحد الأخير = 12 + (5 -1 ) × 2

                    = 12 + 4 × 2

                    = 12 + 8

                    = 20

وبالطريقة نفسها يمكن إيجاد مجموع عدد معين من الأعداد الفردية أو الأعداد المتتالية ومجموع العديد من السلاسل .

وهناك طريقة أخرى تعتمد على الفرق بين الحدين  المتتاليين فالمتسلسلة 12 14 16 18 20

الفرق بين كل حدين متتاليين هو  2 الحد الأول هو 12 .

ويمكن تقديم الفكرة المتسلسلات على فكرة توفير النقود في حصالة. فعلى سبيل المثال  يضع خالد في حصالته نقوداً و أول ما وضع في الحصالة 12 ريال وفي كل يوم يضع 2 ريال زيادة عن اليوم السابق فكم ريالاً يضع في اليوم العاشر ؟ وعند فتح الحصالة بعد عشرة أيام كم ريالا يكون في الحصالة؟