ثانياً- جمع الكسور ذات المقامات المختلفة :

إذا كانت القطعة الصفراء تمثل الوحدة فإنه

+

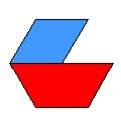
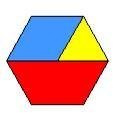
يمكن استبدال القطعة الحمراء بثلاث قطع خضراء أي واستبدال القطعة الزرقاء بقطعتين خضراء أي

+ =

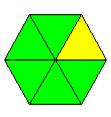
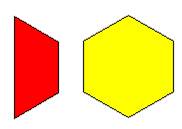
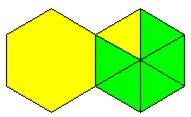
إذا كان الشكل التالي يمثل الوحدة

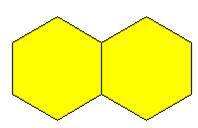
فإن القطعة الصفراء تمثل النصف وقطعتين زرقاء تمثل الثلث والقطعة الحمراء تمثل الربع والقطعة الزرقاء تمثل السدس والقطعة الخضراء تمثل

+

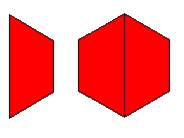
يمكن واستبدال القطعة الصفراء بقطعتين حمراء يصبح لدنيا ثلاث قطع حمراء أي ثلاث أرباع + =

و +

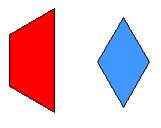
باستبدال القطع الزرقاء بقطعتين خضراء واستبدال القطعة الحمراء بثلاث قطع خضراء يصبح لدينا 5 قطع خضراء أن وعليه فان

+

+ =

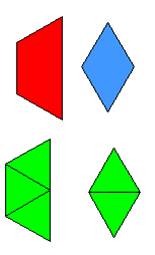
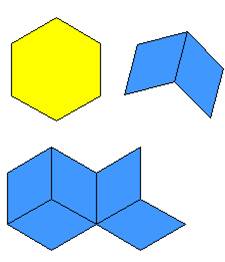
+ نلاحظ أن الثلث يتكون من قطعتين زرقاء أي وباستبدال القطعة الصفراء بثلاث قطع زرقاء أي

+ =

ولذلك لكي نجمع كسرين مختلفين في المقام نوحد المقامين باستخدام المضاعف المشترك الأصغر أو نحو لهما إلى كسرين مكافئين لهما على أن يكون مقامهما مشترك ثم نجمع الكسرين الحاصلين .

لجمع

+

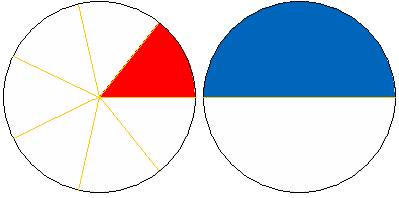
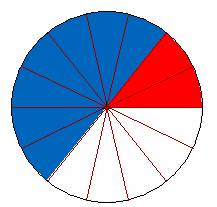
الجزء الملون في الدائرة الأولي يمثل نصف الدائرة بينما يمثل الجزء الملون في الدائرة الثانية سبع الدائرة

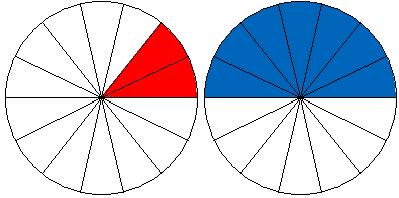
بتقسيم كل دائرة إلي 14 جزء ( لنحصل على مقام مشترك)

نلاحظ أن الجزء الملون في الدائرة الأولى 7 أجزاء من 14 جزءاً أي

والجزء الملون في الدائرة الثانية جزأين من 14 جزءا أي

+ +

وبجمع الكسرين + =

وبالمثل +

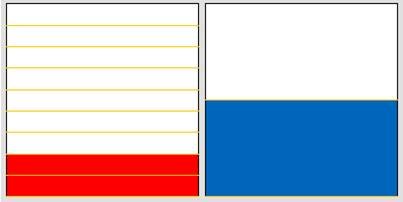
لتوحيد المقامات نضرب بسط ومقام الكسر الأول في 9

وبسط ومقام الكسر الثاني في العدد 2

+

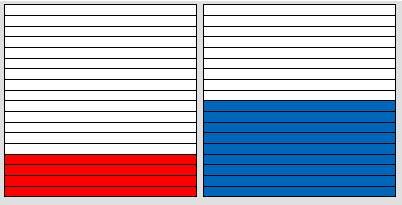
مقام الكسرين موحد ويساوي 18

وبجمع البسطين 9 + 4 = 13

+ =