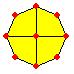
جمع كسر مع عدد صحيح بقطع النماذج

باعتبار أن القطعة الصفراء تمثل الوحدة .

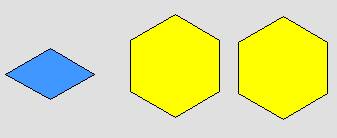
2 +

باستبدال كل قطع صفراء بثلاث قطع زرقاء يصبح لدينا سبع أثلاث

+ + =

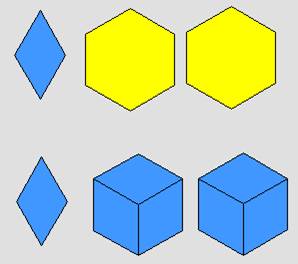
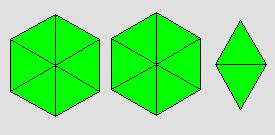
وإذا كانت القطعة الحمراء تمثل الواحد فإن الشكل التالي :

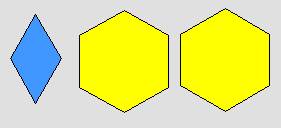
يساوي + 4

باستبدال كل قطعة صفراء بثلاث قطع زرقاء يصبح لدينا سبع قطع زرقاء وكل قطعة زرقاء يمثل الثلثين أي لدينا

أو استبدال كل القطع بقطع خضراء لينتج

+ =

قطع كوزينير

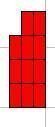
إذا كانت القطعة البنية تمثل الوحدة فإن القطعة الحمراء تمثل الربع ولجمع 2 + نأخذ قطعتين بنيتين وثلاث قطع حمراء .

وباستبدال كل قطعة بنية بأربع قطع حمراء يصبح لدينا ثمان قطع حمراء بالإضافة إلى الثلاثة الأولى. ليصبح مجموع ما لدينا أحد عشر قطعة حمراء كل واحدة تمثل ربع أي

2 +

+ =

المكعبات المتداخلة :

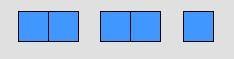
إذا كان كل مكعبين يمثل واحد فإن الشكل السابق يعني + 2

ويفصل كل مكعب عن الآخر ينتج لدينا خمسة أنصاف أي أن

+ 2 =

وبالمثل إذا كانت السلسلة المكونة من 4 مكعبات تمثل الوحدة فإن سلسلة واحدة ومكعب واحد تعني + 1

وبتقسيم السلسلة إلي مكعبات منفصلة يصبح لدينا 5 أرباع :

+ 1 =

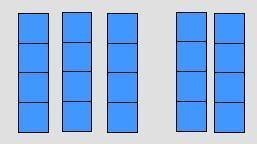
إذا كان الشكل التالي يمثل + 1

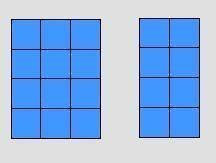
بتقسيم الشكلين إلي أعمدة يصبح لدينا

+ 1

+ =

الميزان الحسابي :

نقوم بتقسيم الذراعين كالتالي :

الأيسر : ، ، ، ، ، ، ، ، ،

الأيمن: ، ، ، ، ، ، ، ، ،

لجمع 1 +

تقوم بوضع ثقل واحد على المشجب الذي يمثل الواحد من الذراع الأيسر ، ووضع ثقل واحد على المشجب الذي يمثل الربع من الذراع الأيسر أيضا ، ثم البحث عن المشجب في الذراع الأيمن الذي يعيد التوازن بالبحث نجد ان

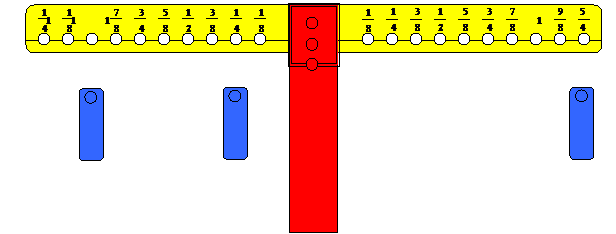
وبالمثل نجمع 1 +

نقوم بوضع ثقل على المشجب الذي يمثل الواحد الصحيح من الذراع الأيسر ، ووضع ثقل واحد على المشجب الذي يمثل الثمن من الذراع الأيسر أيضاً,ثم البحث عن مشجب في الذراع الأيمن يعيد التوازن لنجد أنه

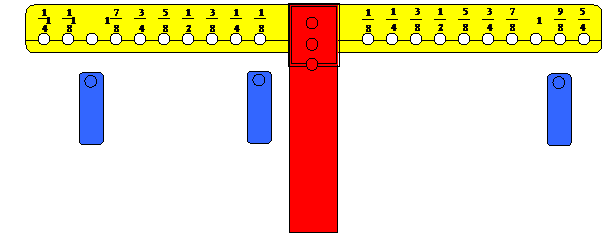
اللوحة الهندسية :

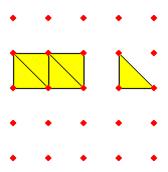
إذا كان كل مربع صغير يمثل وحدة فإن الشكل التالي يمثل :

+ 2

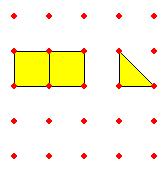
وبتقسيم كل مربع إلى مثلثين يصبح لدينا 5 مثلثات أي 5 إنصاف وعليه فإنه :

+ 2 =

اللوحة الدائرية :

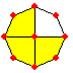
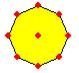
لجمع + 1 تقوم بتجزئة الدائرة إلى تمثل الواحد الصحيح إلى أربعة أجزاء ليصبح مجموع ما لدينا من الأرباع هو سبعة أرباع

+ 1 =