جمع كسرين لهما المقام نفسه .

قطع النماذج

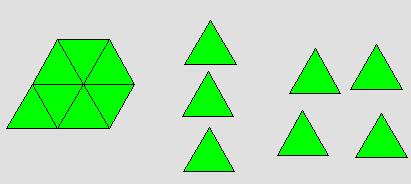
إذا كان الشكل التالي يمثل الوحدة

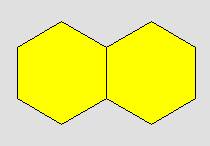
فإن القطعة الصفراء تمثل النصف والقطعة الحمراء تمثل الربع والقطعة الزرقاء تمثل السدس وقطعتين زرقاء تمثل الثلث والقطعة الخضراء تمثل ( ) وعليه فإن

+ = =

+ + =

+ = =

+ = =

+ =

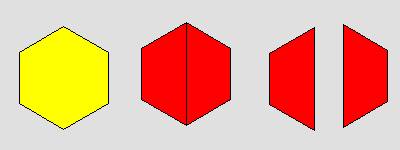
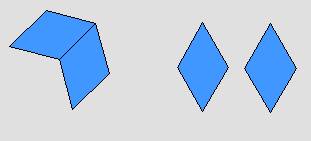
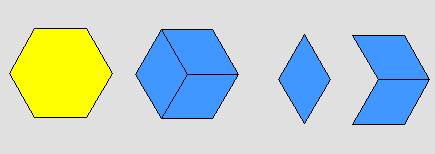
نلاحظ أن :

مجموع كسرين لهما المقام نفسه هو الكسر الذي مقامه يساوي مقام الكسرين ، وبسطة يساوي مجموع بسطيهما .

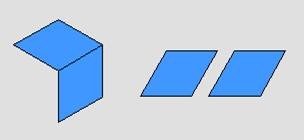
أما إذا كانت القطعة الصفراء تمثل الوحدة فإن

+ =

+ = =

قطع كوزينير :

إذا كانت القطعة السوداء تتمثل الوحدة فإن القطعة البيضاء تمثل السبع :

ونلاحظ أن :

+ =

وبالمثل إذا كانت القطعة الخضراء الغامقة تمثل الوحدة فإن القطعة الحمراء تمثل الثلث وعليه فإن :

+ =

المكعبات المتداخلة :

بناء سلسلة مكونة من ستة مكعبات ، 3 مكعبات خضراء وتمثل ثلاث أسداس السلسلة ، ومكعبين أصفرين ويمثلان سدسين السلسلة ومكعب أحمر يمثل سدس السلسلة وعليه فإن :

الكسر الذي يمثل مجموع المكعبات الحمراء والصفراء هو

+ =

والكسر الذي يمثل مجموع المكعبات الصفراء والخضراء هو

+ =

والكسر الذي يمثل مجموع المكعبات الخضراء والصفراء هو

+ =

الميزان الحسابي

لجمع : +

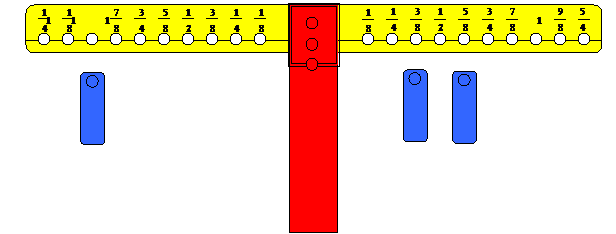
يتم تمثيل الكسر الأول بوضع ثقل واحد على المشجب الذي يمثل ثلاثة أثمان من الذراع الأيمن ووضع ثقل واحد على الذراع الذي يمثل خمسة أثمان من الذراع نفسه ، ثم البحث عن المشجب في الذراع الأيسر الذي يمثل المجموع عند وضع ثقل عليه ويعيد التوازن .

وعند البحث نجدان المشجب الذي يمثل الواحد أي

اللوحة الهندسية :

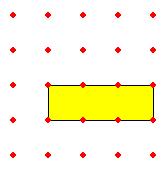
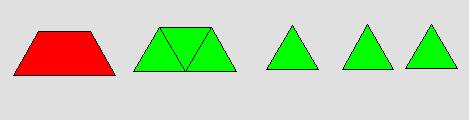
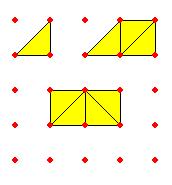
إذا كان الشكل السابق يمثل الوحدة فإن كل مثلث يمثل ربع المستطيل, مثلثين معاً يمثلان ربعي (نصف) الشكل ويشكلان مربع وأن 3 مثلثات تمثل ثلاث أرباع الشكل وتشكل شبه منحرف

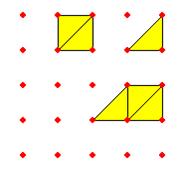
لذا فإن مثلث مع مثلث تشكل مربع أي أن :

+ =

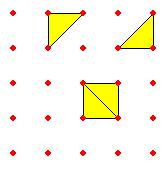
وأن مربع مع مثلث يشكل شبه منحرف

+ =

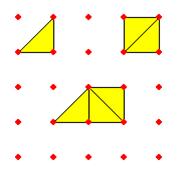
وأن شبه منحرف مع مثلث يشكل المستطيل أي أن :

+ =

اللوحة الدائرية :

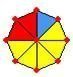
بتقسيم الدائرية إلى ثمان أقسام نلاحظ أن :

+ =

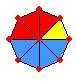
وبالمثل + =